Стороны основания правильной треугольной пирамиды равна 18 дм,а площадь её боковой поверхности равна 162 дм^2. Найти объем пирамиды. Помогите пожалуйста.
Ответы
Ответ дал:
0
Площадь боковой поверхности S=P·l/2=3a·l/2, где l - апофема.
l=2S/3a=2·162/(3·18)=6 дм.
Апофема l, радиус вписанной в основание окружности r и высота пирамиды h образуют прямоугольный треугольник.
h=√(l²-r²).
В правильном треугольнике r=a√3/6=18√3/6=3√3 дм.
S=a²√3/4=18²√3/4=81√3 дм².
h=√(6²-(3√3)²)=3 дм.
Объём пирамиды V=Sh/3=81√3·3/3=81√3 дм³ - это ответ.
l=2S/3a=2·162/(3·18)=6 дм.
Апофема l, радиус вписанной в основание окружности r и высота пирамиды h образуют прямоугольный треугольник.
h=√(l²-r²).
В правильном треугольнике r=a√3/6=18√3/6=3√3 дм.
S=a²√3/4=18²√3/4=81√3 дм².
h=√(6²-(3√3)²)=3 дм.
Объём пирамиды V=Sh/3=81√3·3/3=81√3 дм³ - это ответ.
Ответ дал:
0
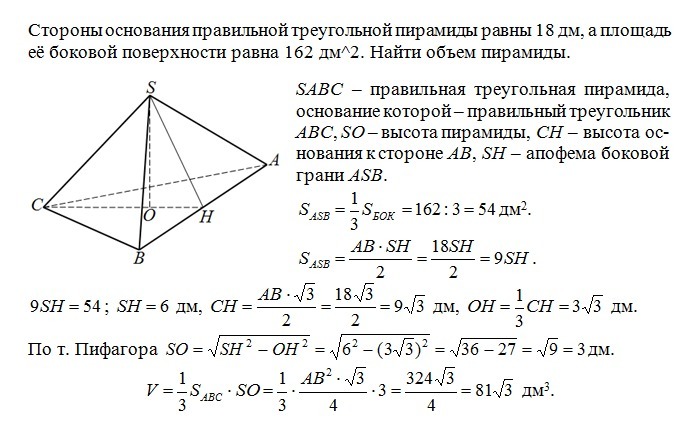
Решение в приложении.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад