Ответы

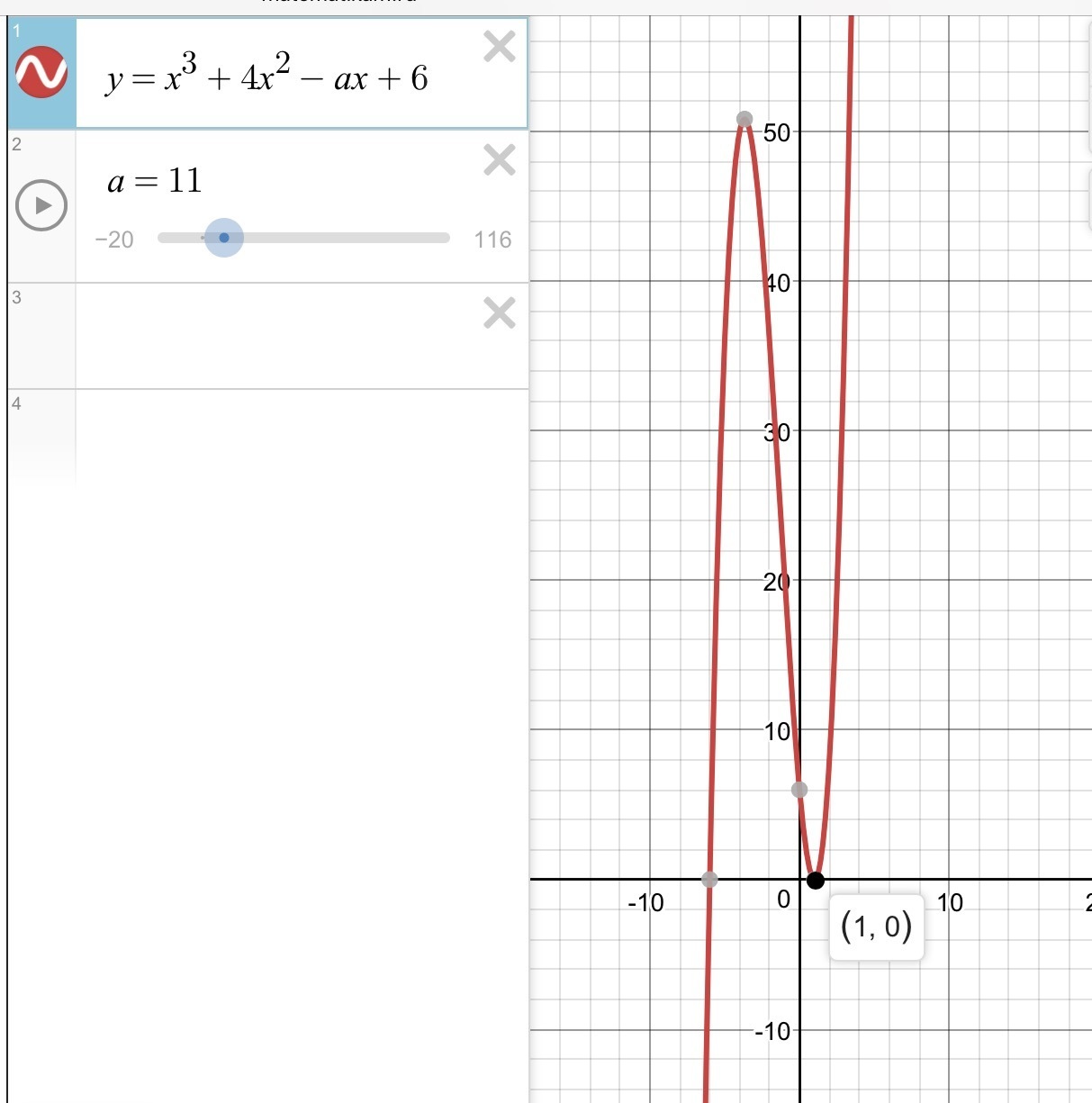
уравнение x^3+4x^2−kx+6=0 на отрезке x∈[−2;2] , где k=log2(b−3)
Достаточно найти значения k, при которых выполняется условие единственности решения.
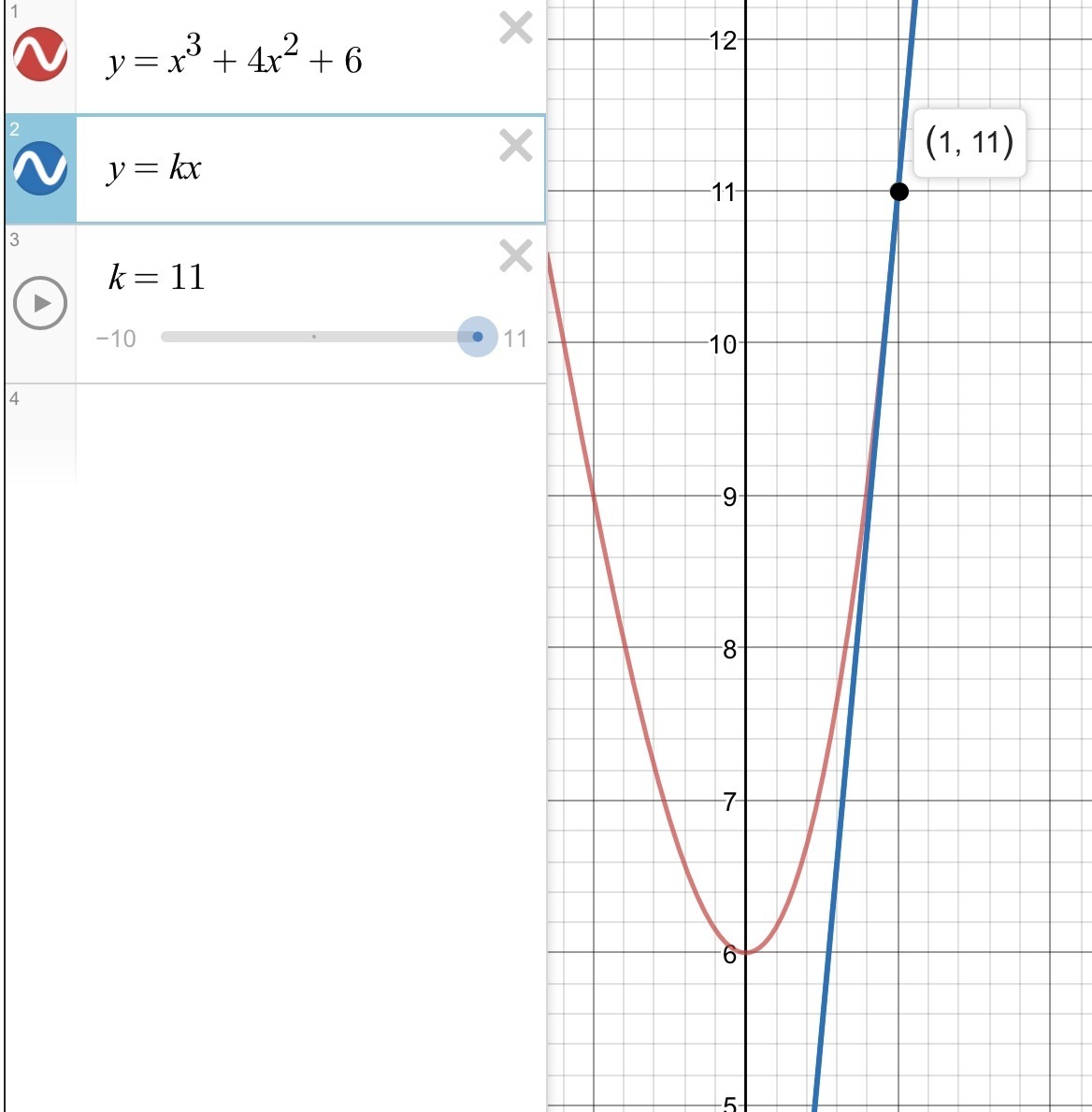
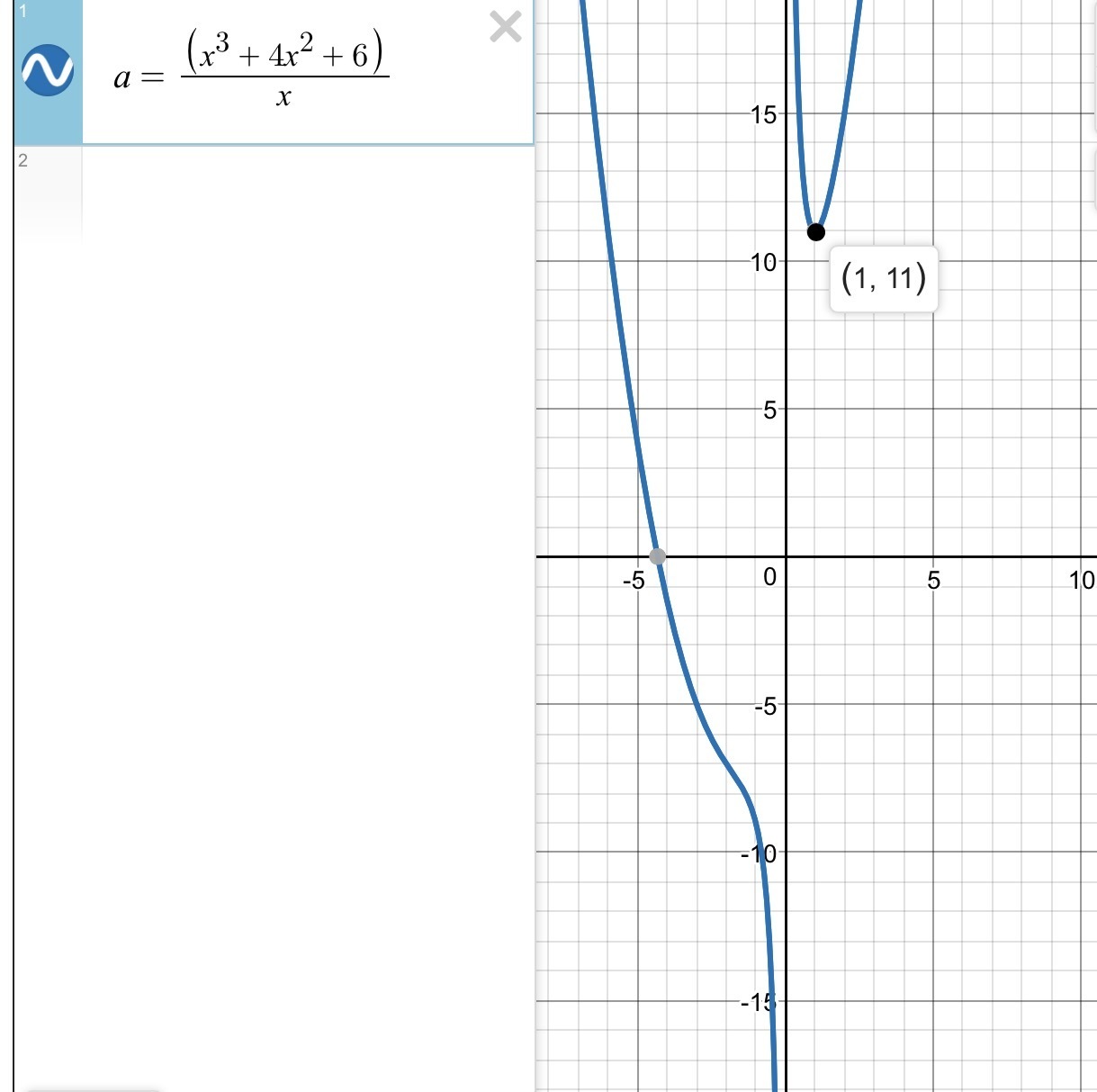
Запишем уравнение в виде x^3+4x^2+6=kx, и построим на отрезке график функции y=x^3+4x^2+6=0
Рассмотрим случай, когда решение x положительно.
Исследуем случай, когда прямая y=kx касается графика в некоторой точке.
Угловой коэффициент касательной равен y′(x)=3x^2+8x=k
⇒ 3x^3+8x^2=kx=x^3+4x^2+6
⇒ x^3+2x^2−3=0 корнем которого является число x=1
x^3+2x^2−3=(x−1)(x^2+3x+3)=0 , где квадратный трёхчлен корней не имеет. (D<0)
Это значит, что кроме x=1 других решений нет.
При этом k=11
из графиков видно, что при 0≤k≤11 решений нет,
при k=1 решение одно
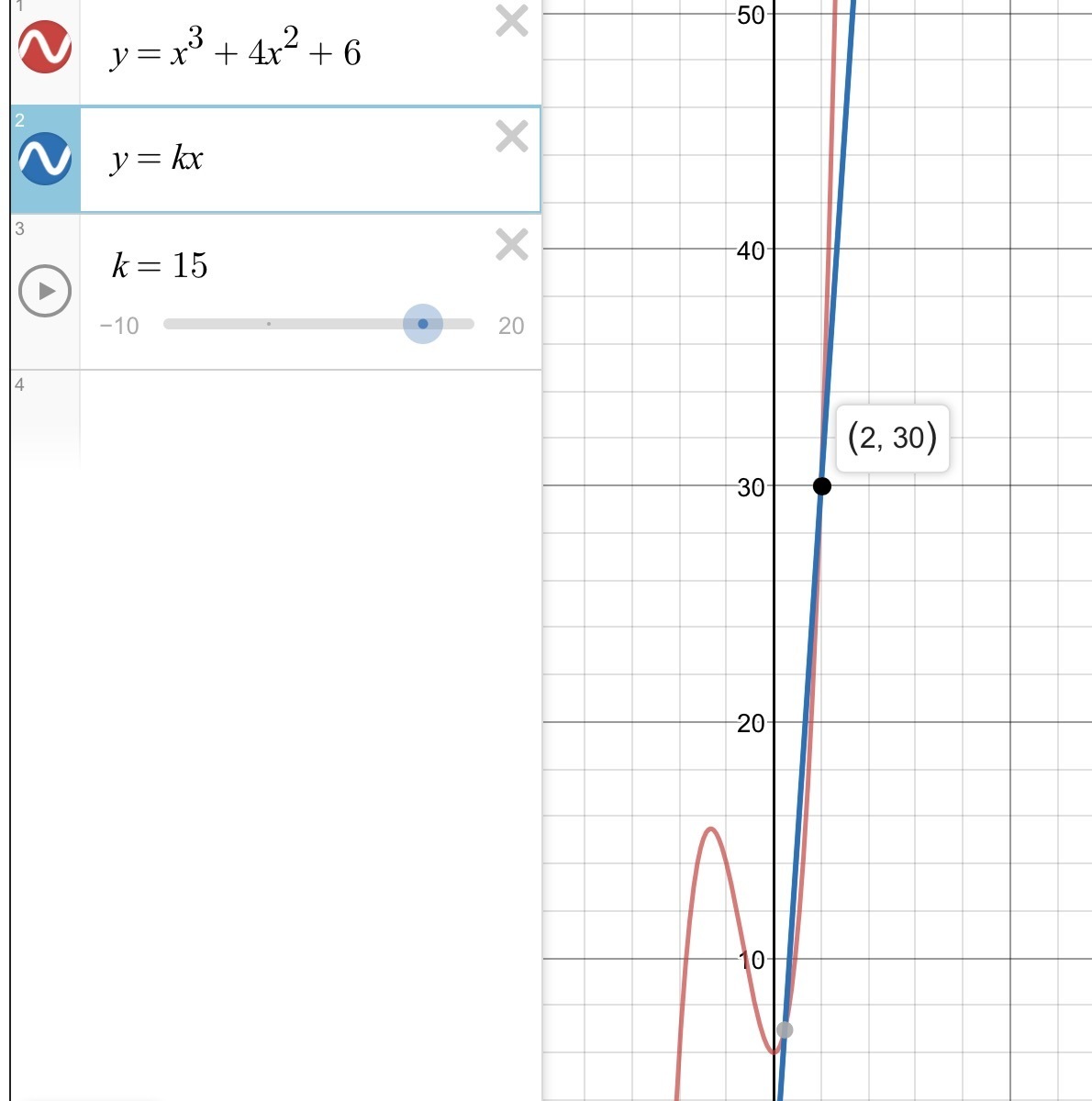
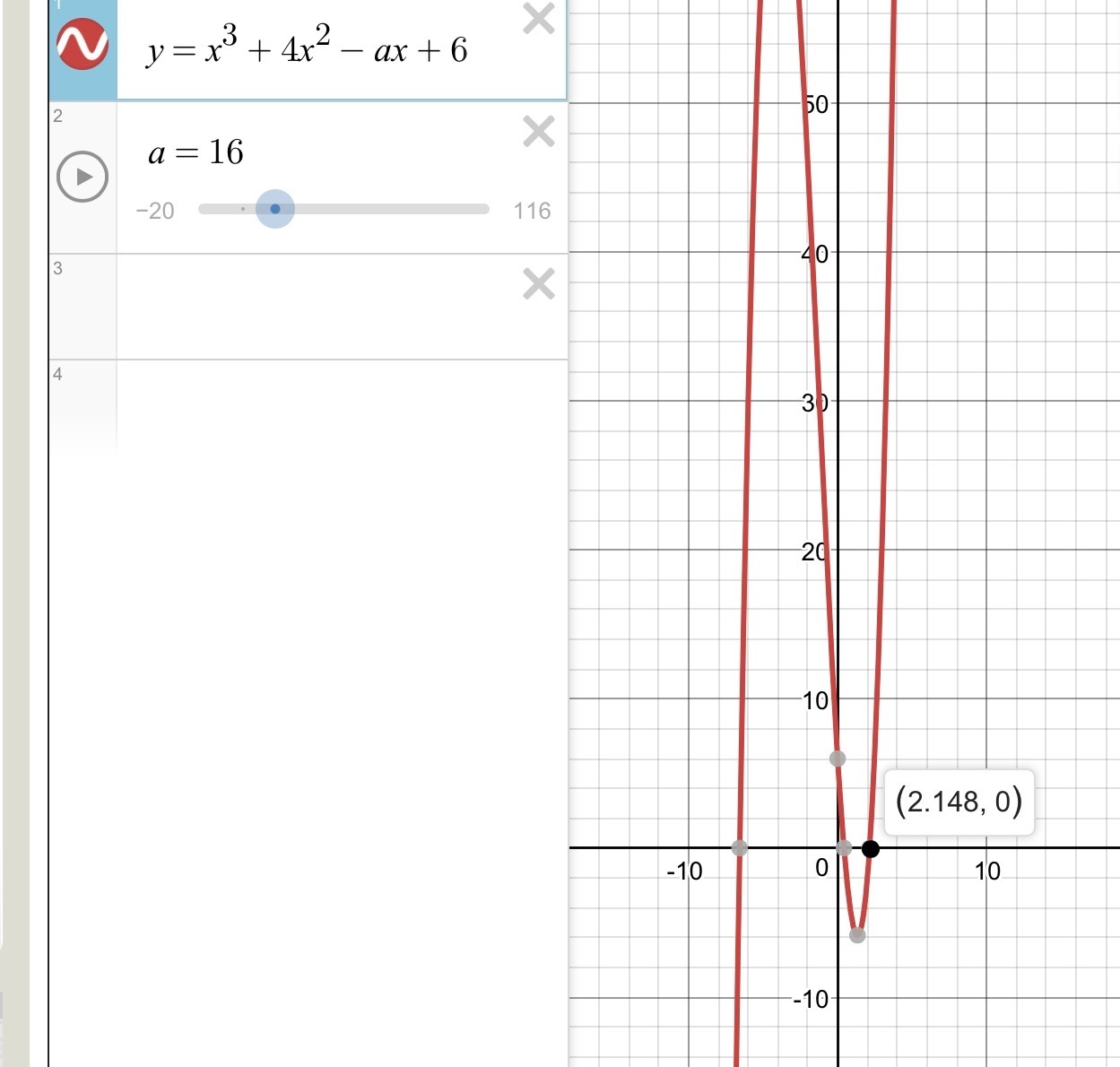
при 11<k≤15 решений два
при k>15 решение будет одно.
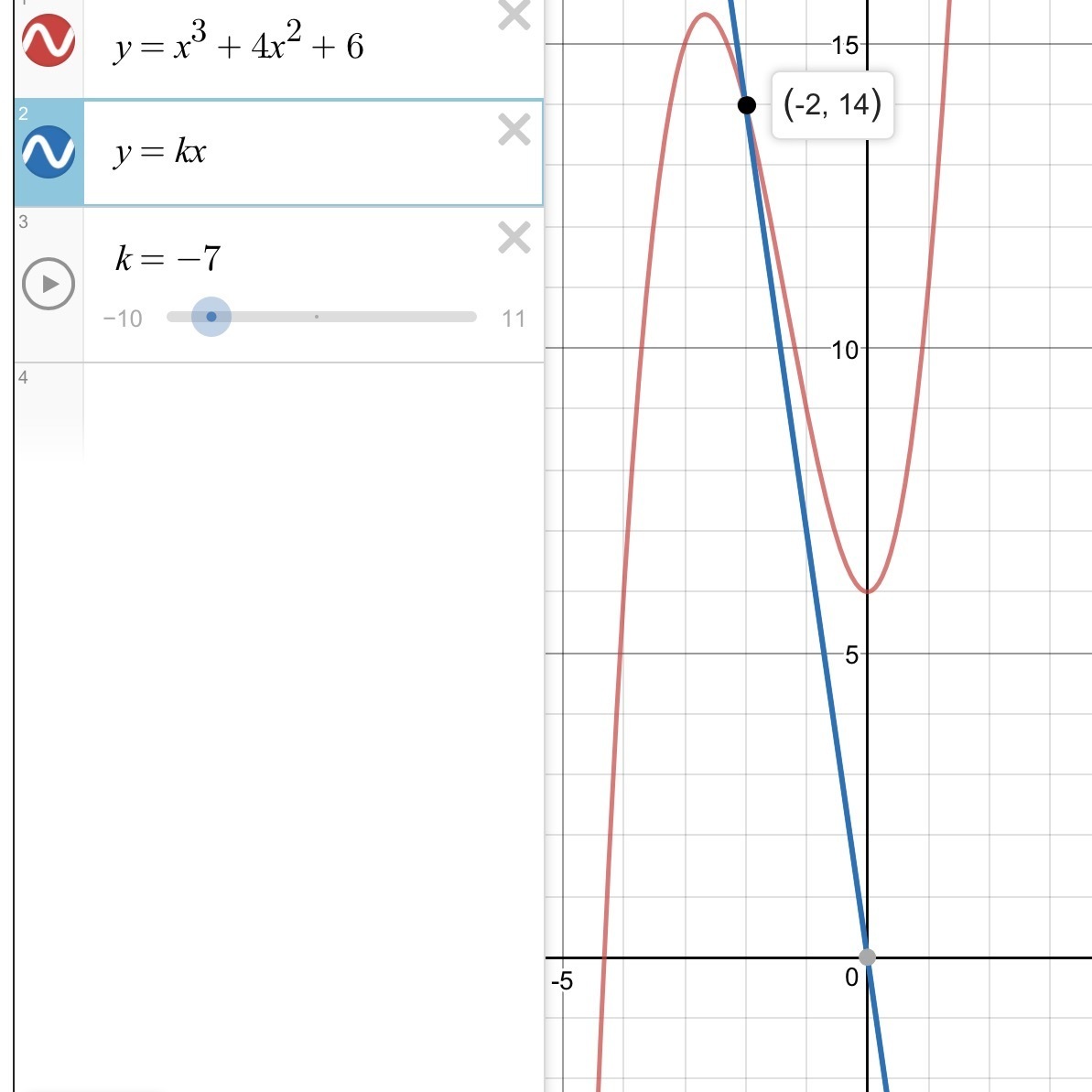
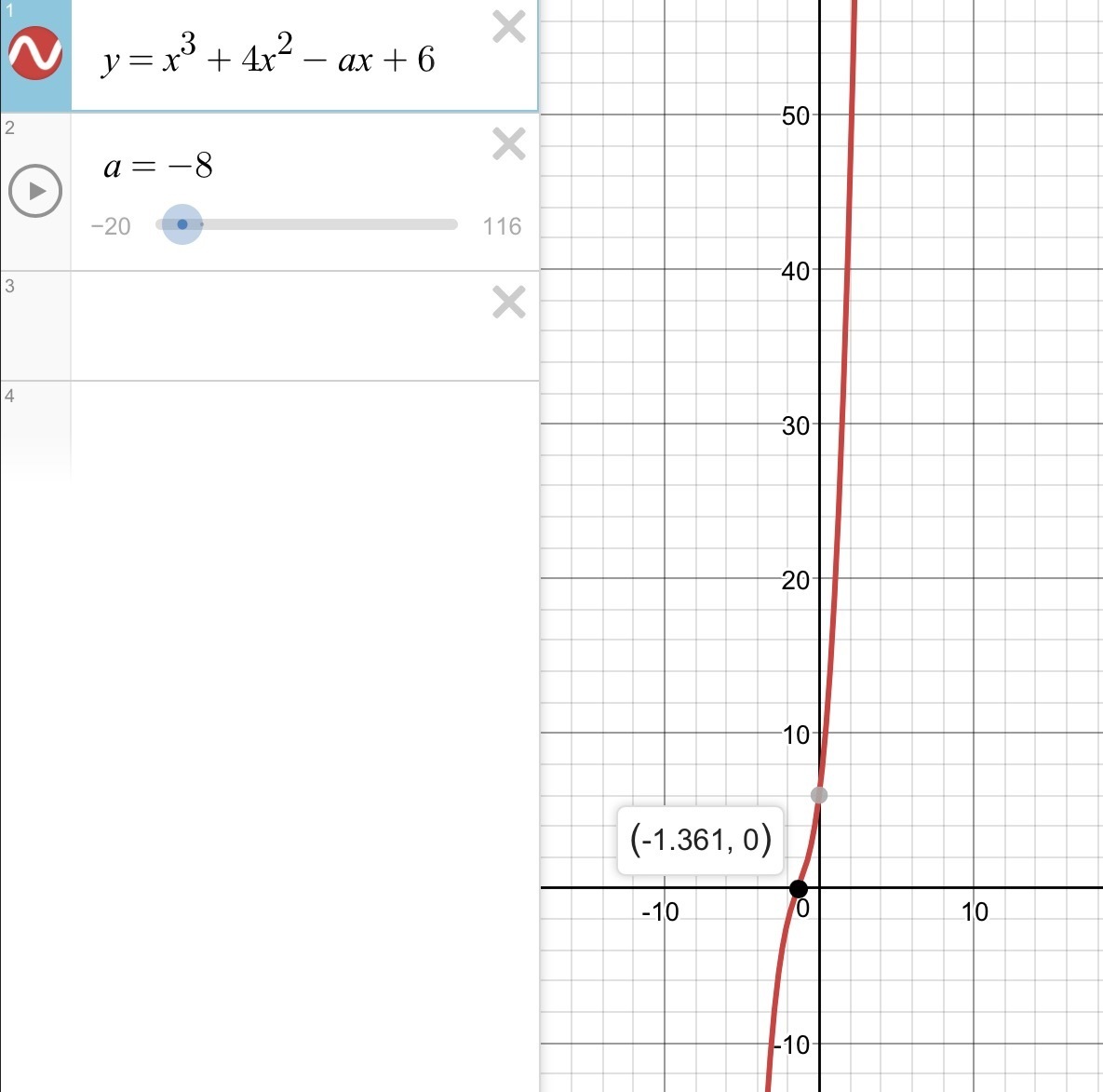
Если k<0, то касание невозможно, и график прямой один раз пересекает график кубического многочлена при k≤−7.
Таким образом, k∈(−∞;−7)∪{11}∪(15;+∞)
Отсюда 0<b−3≤2^(−7), или b−3=2^11, или b−3>2^15
Это значит, что b∈(3;385/128]∪{2051}∪(32771;+∞)