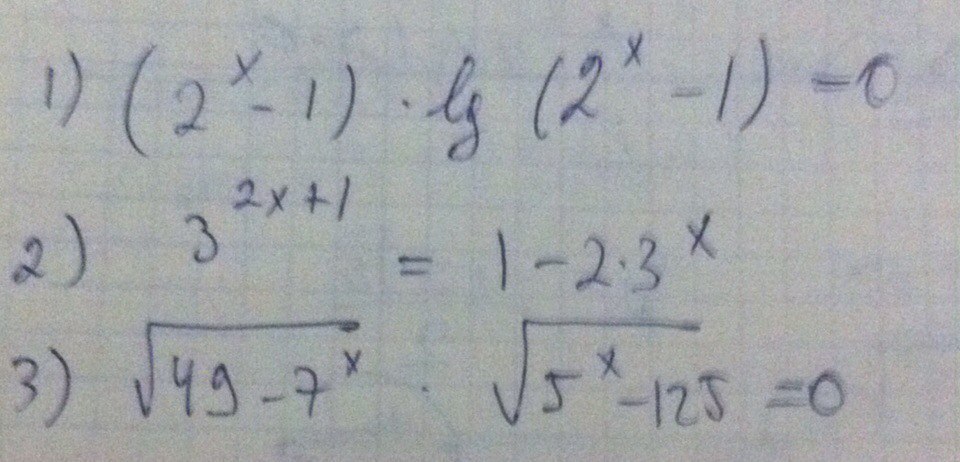Question

пожалуйста, помогите решить уравнения

Answer 1

1. (2^x-1)*lg(2^x-1)=0
один из сомножителей равен 0 
но для начала для логарифма надо всегда находить одз
2^x>1  x>0
Одз x⊂(0 +∞)
 первый сомножитель
2^x-1=0
2^x=1
x=0 НЕТ по ОДЗ
второй сомножитель
lg(2^x-1)=0
2^x-1=1
2^x=2
x=1 ДА
ответ 1
---------------------------------------------------
3^(2x+1) = 1 - 2*3^x 
3*3^(2x) + 2*3^x - 1=0
3^x=t t>0
3t²+2t-1=0
D=4+12=16=4²
t12=(-2+-4)/6 = 1/3  -1
t₂=-1  Нет
t₁=1/3
обьратная замена
3^x=1/3

3^x=3^(-1)
x=-1
ответ  -1
----------------------------------------------
3) как и первом умножение один из сомножителей равен 0
Но в корнях четной степени снова ОДЗ подкоренное выражение≥0
49-7^x≥0    7^x≤7^2    x≤2
5^x-125≥0   5^x ≥ 5^3  x≥3  это система не имеет решений, значит и уравнение не имеет решений
Если смотреть равенство 0 первого радикала x=2 то второй 25-125<0
второго радикала x=3 то первый 49-243<0
ответ решений нет

Answer 2

еще раз спасибо)

Answer 3

вы хоть перепроверяйте решения. мы все ошибиться можем. мы не боги безгрешные

Answer 4

я решаю сам, потом сравниваю со своим решением и ответом