Нужно исследовать функцию: y=x³-3x²
Помогите. Зачет, а я лох. Желательно на листике, чтобы было понятно.
Ответы
Ответ дал:
0
1)Область определения функции:

2) Определение четности/нечетности и периодичности функции:

Функция общего вида.
Функция непериодична.
3) Асимптоты, поведение функции на бесконечности:
Асимптот тут нет, т.к. функция обыкновенная и без дробной части.
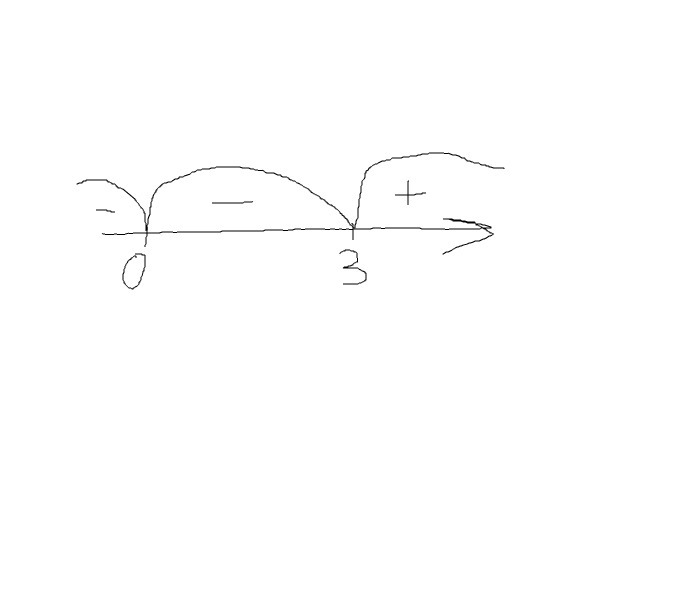
4) Нули функции и интервалы знакопостоянства:
Точка пересечения графика с осью ординат:

С осью абцисс:






Интервалы знакопост. смотри в первом рис.
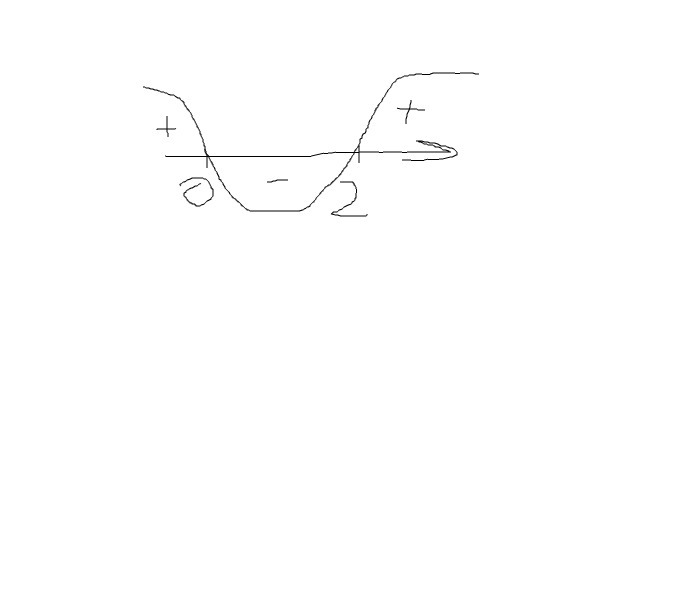
5) Возрастание, убывание и экстремумы функции:
Критические точки:






Интервалы промежутков смотри во втором рисунке.
На промежутках (-беск.; 0) и (2; +беск) - функция возрастает, а на (0;2) убывает.
 - максимум функции.
- максимум функции.
 - минимум функции.
- минимум функции.
6) Выпуклость, вогнутость и точки перегиба.




Знаки y'' смотри на 3 рисунке.
График является выпуклым на (-беск.; 1) и вогнутым на (1; +беск)
Ордината точки перегиба:

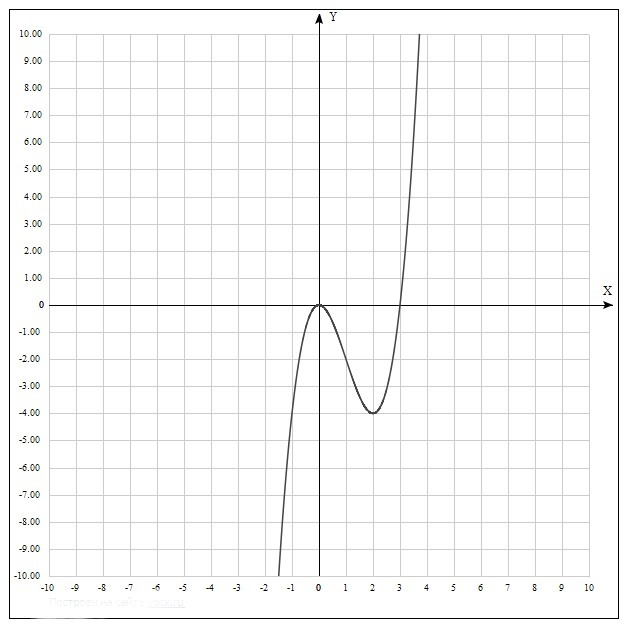
7) Построение графика функции.
Смотри на рисунке 4.
2) Определение четности/нечетности и периодичности функции:
Функция общего вида.
Функция непериодична.
3) Асимптоты, поведение функции на бесконечности:
Асимптот тут нет, т.к. функция обыкновенная и без дробной части.
4) Нули функции и интервалы знакопостоянства:
Точка пересечения графика с осью ординат:
С осью абцисс:
Интервалы знакопост. смотри в первом рис.
5) Возрастание, убывание и экстремумы функции:
Критические точки:
Интервалы промежутков смотри во втором рисунке.
На промежутках (-беск.; 0) и (2; +беск) - функция возрастает, а на (0;2) убывает.
6) Выпуклость, вогнутость и точки перегиба.
Знаки y'' смотри на 3 рисунке.
График является выпуклым на (-беск.; 1) и вогнутым на (1; +беск)
Ордината точки перегиба:
7) Построение графика функции.
Смотри на рисунке 4.
Приложения:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад