Question

Высота правильной четырехугольной призмы равна h. Прямая,соединяющая центр верхнего основания с серединой стороны нижнего основания ,наклонена к плоскости нижнего основания под углом L(альфа). Найти площадь полной поверхности призмы.

Answer 1

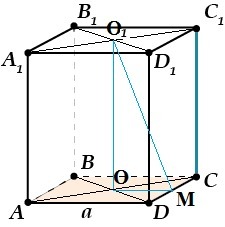
Основаниями правильной четырехугольной призмы являются квадраты со стороной а. Точки О и О₁ являются центрами соответствующих оснований. 

В прямоугольном треугольнике O₁MO:
катет ОМ = а/2
катет OO₁ = H
∠O1MO = α
Отношение прилежащего к углу ∠O1MO катета ОМ к противолежашему катету OO₁ является котангенсом угла ∠O1MO 
                ОМ 
ctg α = -------------
                OO₁

                 a
ctg α = ---------
                2H

a = 2H * ctg α

Площадь полной поверхности призмы равна сумме площадей поверхностей боковых граней и оснований

Sполн = Sбок + 2Sосн

Sосн = а²
Sосн = (2H * ctg α)²
Sосн = 4H² * ctg²α

Sбок = P * H, где P  - перметр основания
Sбок = 4а * H
Sбок = 4 * 2H * ctg α * H

Sполн = 4 * 2H * ctg α * H + 2 * 4H² * ctg²α = 
= 8H² * ctg α + 8H² * ctg²α = 8H² (ctg α + ctg²α)