Ответы
Ответ дал:
0
Найдем ограниченные линии

По т. Виета:
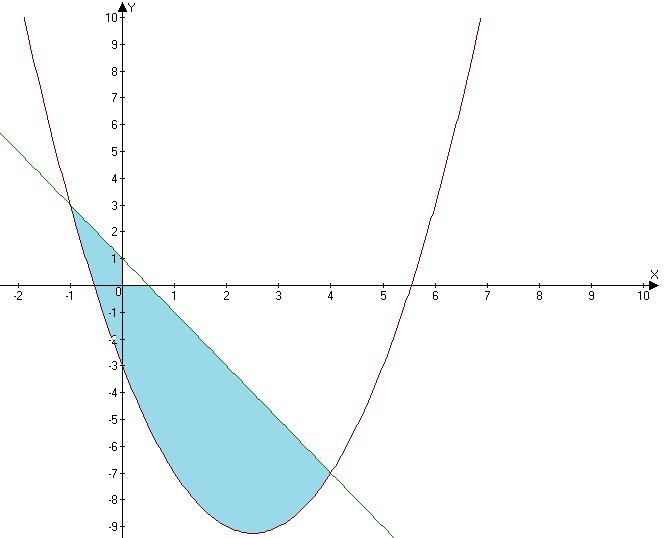
Графиком функции y=x²-5x-3 является парабола, ветви направлены вверх.
y=1-2x - прямая, которая проходит через точки (1;0) и (0.5;1)
График функции y=x²-5x-3 расположен ниже прямой y=1-2x.
Значит площадь фигуры будем вычислять след образом

По т. Виета:
Графиком функции y=x²-5x-3 является парабола, ветви направлены вверх.
y=1-2x - прямая, которая проходит через точки (1;0) и (0.5;1)
График функции y=x²-5x-3 расположен ниже прямой y=1-2x.
Значит площадь фигуры будем вычислять след образом
Приложения:
Вас заинтересует
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад
