Question

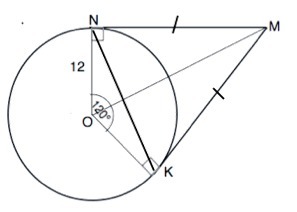
Из точки М к окружности с центром O и радиусом 12 см проведены касательные MK и MN (K и N-точки касания). Найдите периметр треугольника MNK, если градусная мера дуги KN равна 120гр.

Answer 1

Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. 

Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. 

Отсюда следует равенство Δ ONM=Δ OKM.

Угол КОМ=120°:2=60°, КМ=MN=ОК•tg60°=12√3

Сумма углов четырехугольника 360°.

Поэтому ∠NMK=360°-2•90°-120°=60°

Треугольник NMK равнобедренный с углом при вершине М, равным 60°. Значит, углы при основании NK равны по 60° каждый. 

Треугольник MNK- равносторонний. Р=3МК=3•12√3=36√3 (ед. длины)