ПОМОГИТЕ ПОЖАЛУЙСТА
Решите уравнение
sinx+sin3x/cosx+cos3x=0
на картинке 9 задание
Приложения:
Дальше я запутался. Прости.
Ого. Спасибо большое
Та не за шо) Сильная задачка, затянула)
Ответы
Ответ дал:
0
нужно с начало упростить
Приложения:
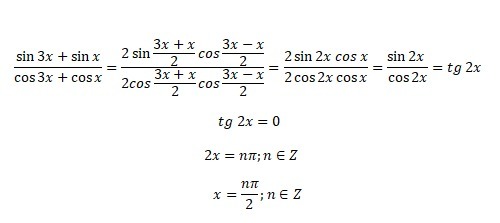
сначала
Вас заинтересует
1 год назад
1 год назад
1 год назад
8 лет назад
1/2 * (sin 4x + sin -2x) + 1/2 (sin4x + sin 2x).
cosx+ cos3x = cos x * cos 3x + sin3x*sin x =>
1/2 * (cos -2x + cos 4 x) + 1/2 (cos 2x - cos 4x).
2 sin 4 x= 4 sinx * cos x
1/2 ( (sin 4x +sin -2x + sin 4x + sin 2x) / (cos -2x + cos 4x + cos 2x - cos 4x) )= 1/2 ( (2 sin 4x + sin -2x + sin 2x) / (cos -2x+ cos 2x) ) =>
4 sin2x * cos2x + sin -2x + sin 2x / cos 2x + cos -2x =>
sin 2x (4 cos2x + 1) + sin -2x/ cos 2x + cos -2x =>