найдите три решения уравнение помогите пожалуйста!!!!! даю много баллов только решите!
Приложения:
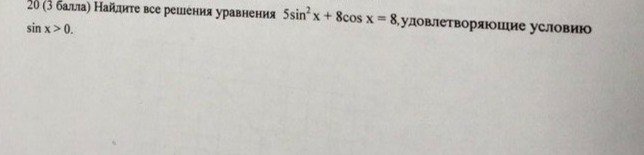
Ответы
Ответ дал:
1
5sin^2(x)+8cos(x)=8
8-5sin^2(x)-8cos(x)=0
2.5-5sin^2(x)+5.5-8cos(x)=0
5cos^2(x)+3-8cos(x)=0
cos(x)=(8+-sqrt(64-60))/10=(8+-2)/10= 1 или 0,6
Значит:
x = 2 π n, n ∈ Z
x = 2 π k - arccos(3/5), k ∈ Z
x = 2 π k + arccos(3/5), k ∈ Z
Но sin(x)>0
Тогда:
x = 2 π k + arccos(3/5), k ∈ Z
8-5sin^2(x)-8cos(x)=0
2.5-5sin^2(x)+5.5-8cos(x)=0
5cos^2(x)+3-8cos(x)=0
cos(x)=(8+-sqrt(64-60))/10=(8+-2)/10= 1 или 0,6
Значит:
x = 2 π n, n ∈ Z
x = 2 π k - arccos(3/5), k ∈ Z
x = 2 π k + arccos(3/5), k ∈ Z
Но sin(x)>0
Тогда:
x = 2 π k + arccos(3/5), k ∈ Z
Leo565:
а можно подробней а то не очень понятно откуда берутся 2.5 и 5.5
и 64-60
8=2.5+5.5
sqrt(D)=sqrt(b^2-4ac)=8^2-4*5*3=64-60
Это квадратное уравнение. Только вместо 5x^2 5cos^2(x). Кстати, можно пояснить еще, что 1 и 0.6 ВХОДЯТ в множество значений cos(x), так как могло так и не получится. Но это и так видно.
Спасибо большое
Вас заинтересует
1 год назад
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад