Найдите сторону равностороннего треугольника, если его высота равна 6 см. Только более потробно в решении самого уравнения и если можно то и с рисунком
Ответы
Ответ дал:
0
Пусть дан ΔАВС
АВ = ВС = АС
СН - высота
СН = 6
Найти АС.
В равностороннем треугольнике высота является медианой, отсюда:
АН = АВ/2 (отрезок АН равен половине стороны треугольника АВС)
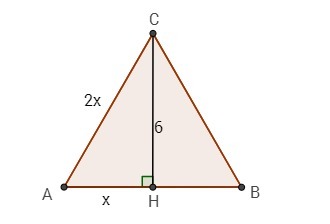
Пусть АН = х, тогда АС = 2х, по теореме Пифагора:
(2х)² - х² = 6²
4х²-х²=36
3х²=36
х²=12
х=√12=2√3
АС = 2х = 2 * 2√3 = 4√3.
АВ = ВС = АС
СН - высота
СН = 6
Найти АС.
В равностороннем треугольнике высота является медианой, отсюда:
АН = АВ/2 (отрезок АН равен половине стороны треугольника АВС)
Пусть АН = х, тогда АС = 2х, по теореме Пифагора:
(2х)² - х² = 6²
4х²-х²=36
3х²=36
х²=12
х=√12=2√3
АС = 2х = 2 * 2√3 = 4√3.
Приложения:
Ответ дал:
0
Высота равностороннего треугольника - h=a√3/2?где а - сторона треугольника.
а=2h/√3;
а=2*6/√3=12/√3=12√3/3=4√3.
а=2h/√3;
а=2*6/√3=12/√3=12√3/3=4√3.
Приложения:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад