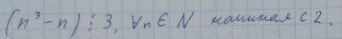Ответы
Ответ дал:
1
1) пусть n=2
верно
2) пусть верно для n=k
тогда проверим для n=k+1
Мы видим три последовательных числа
значит одно из них даст кратность 3
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n≥2
ЧТД
schkud:
Спасибо огромное
Кстати, факт верен для любого целого n, а метод математической индукции здесь не используется, да он и не нужен. Но если поставить цель его использовать, можно взять разность ((k+1)^3-(k+1))-(k^3-k)=3k^2+3k=3(k^2+k)
Да, Юрий Вы правы.. но раз просят таким методом.. так и доказали))
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад