Question

Решить уравнение: cos^2(x)-cos(2x)=0,75 и найти все корни, принадлежащие промежутку [-2П;-П/2]

Answer 1

cos²x - (2cos²x - 1) = 3/4
- cos²x + 1 = 3/4
cos²x = 1/4
cosx = 1/2          или              cosx = - 1/2
x = π/3 + 2πn                         x =  2π/3 + 2πk
x = - π/3 + 2πm                       x = - 2π/3 + 2πl
Группы корней можно объединить:
x = π/3 + πn
x =  - π/3 + πk
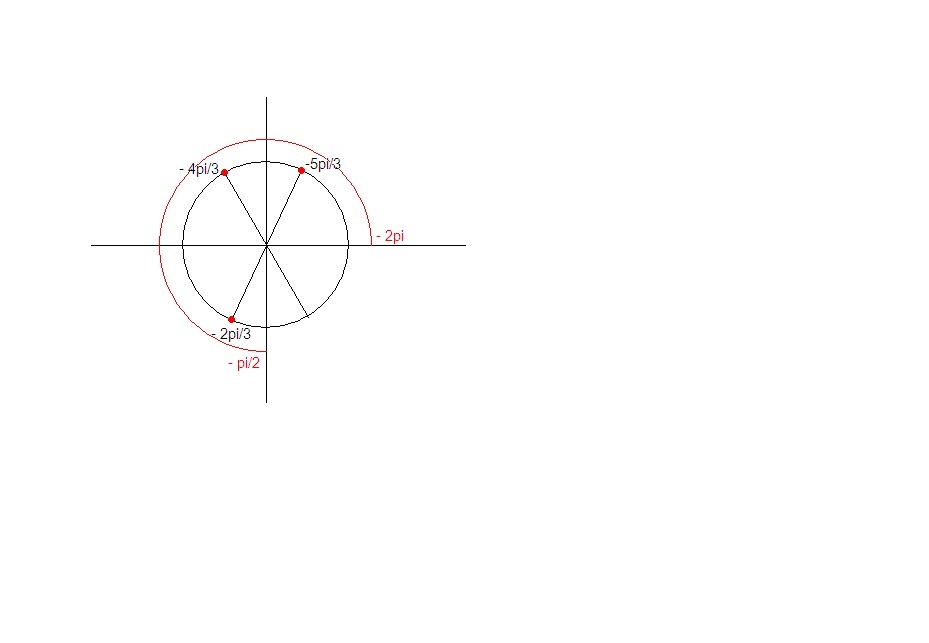
 На промежуток [ - 2π ; - π/2] попали корни
- 2π/3;  - 4π/3;  - 5π/3