Ответы
Ответ дал:
0
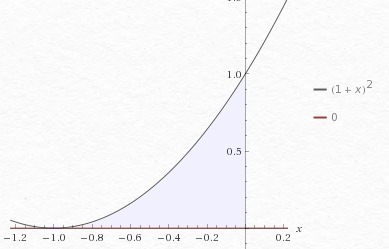
у=(х+1)^2, у=0 (ось оX)
, х=0
S=
найдем 2-й предел
(x+1)^2=0
x=-1
S=∫0,-1(x+1)^2dx=|0,-1((x+1)^3)/3=1/3-0=1/3
, х=0
S=
найдем 2-й предел
(x+1)^2=0
x=-1
S=∫0,-1(x+1)^2dx=|0,-1((x+1)^3)/3=1/3-0=1/3
Приложения:
Ответ дал:
0
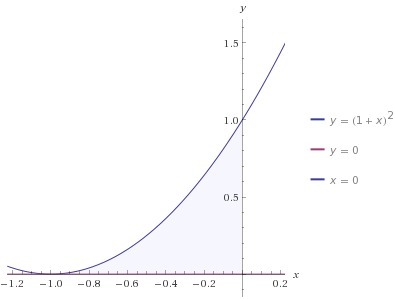
первый предел есть: x=0
ищем 2 предел:
(x+1)^2=0
x+1=0
x=-1
(x+1)^2=x^2+2x+1
находим площадь с помощью определенного интеграла:

Ответ:
ищем 2 предел:
(x+1)^2=0
x+1=0
x=-1
(x+1)^2=x^2+2x+1
находим площадь с помощью определенного интеграла:
Ответ:
Приложения:
Вас заинтересует
2 года назад
2 года назад
9 лет назад
9 лет назад