Дана правильная четырехугольная пирамида, боковое ребро которой равно 5,а диагональ основания равна 6.Найдите объем пирамиды
Ответы
Ответ дал:
0
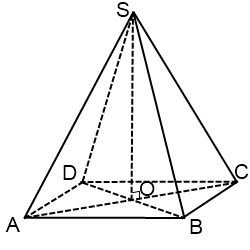
Дано:  - правильная четырехугольная пирамида. SO - высота пирамиды. AC = 6, SC=SD=SA=SB = 5.
- правильная четырехугольная пирамида. SO - высота пирамиды. AC = 6, SC=SD=SA=SB = 5.
Найти: V
Решение:
Диагонали основания ABCD пересекаются в точке О и точка О делит диагональ АС пополам, то есть AO = OC = AC/2 = 3.
Из треугольника SAO(∠SOA=90градусов):
По т. Пифагора:

Площадь основания:
Тогда объем пирамиды:

Найти: V
Решение:
Диагонали основания ABCD пересекаются в точке О и точка О делит диагональ АС пополам, то есть AO = OC = AC/2 = 3.
Из треугольника SAO(∠SOA=90градусов):
По т. Пифагора:
Площадь основания:
Тогда объем пирамиды:
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад