Решите треугольник по двум сторонам и углу, заключенному между ними. Заранее спасибо!
Приложения:
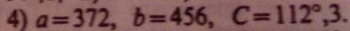
Ответы
Ответ дал:
0
все остальные элементы можно найти лишь приближенно:
найдем сторону "с" по теореме косинусов:

 ≈ 475056
≈ 475056
 ≈ 689
≈ 689
теперь найдем угол А (напротив стороны а) по теореме синусов:

 ≈ 0.5
≈ 0.5
∠А=30°
∠B=180°-(∠A+∠C)=180°-(30°+112.3°)=37.7°
Ответ: В≈689; ∠А≈30°; ∠B≈37.7°
найдем сторону "с" по теореме косинусов:
теперь найдем угол А (напротив стороны а) по теореме синусов:
∠А=30°
∠B=180°-(∠A+∠C)=180°-(30°+112.3°)=37.7°
Ответ: В≈689; ∠А≈30°; ∠B≈37.7°
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад