Question

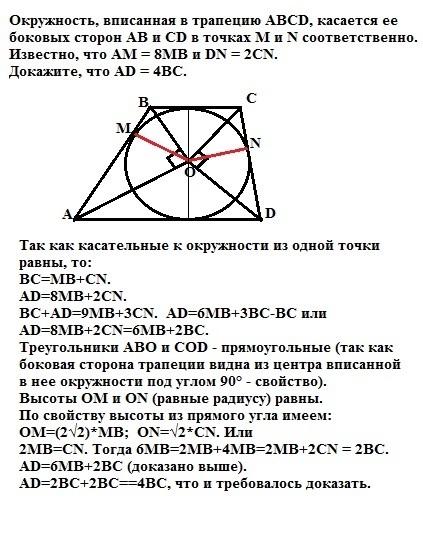
Окружность, вписанная в трапецию ABCD, касается ее боковых сторон AB и CD в точках M и N соответственно. Известно, что AM = 8MB и DN = 2CN.
Докажите, что AD = 4BC.
С рисунком.

Answer 1

а) Пусть окружность касается оснований BC и AD в точках K и L соответственно, а ее центр находится в точке O.

Лучи AO и BO являются биссектрисами углов BAD и ABC соответственно, поэтому <BAO+<ABO=(<BAD+<ABC)/2=90

Значит треугольник AOB прямоугольный. Аналогично, треугольник COD тоже прямоугольный. Пусть BM = x, CN = y, тогда AM = 8x, DN = 2y

MO=√AM*MB=2√2x=NO=√CN*ND=3y

Отсюда у=2х

Следовательно

BK=BM=x

AL=AM=8x

CK=CN=2x

DL=DN=4x

BC=BK+KC=3x

AD=AL-LD=12x

ОтсюдаAD=4BC

0fef07f090a1b103d24053e00729d90c.docx

Answer 2

Так как касательные к окружности из одной точки равны, то:
ВС=МВ+CN.
AD=8MB+2CN.
BC+AD=9MB+3CN.  AD=6MB+3BC-BC или
AD=8MB+2CN=6MB+2BC.
Треугольники АВО и СОD - прямоугольные (так как боковая сторона трапеции видна из центра вписанной в нее окружности под углом 90° - свойство).
Высоты ОМ и ОN (равные радиусу) равны.
По свойству высоты из прямого угла имеем:
ОМ=(2√2)*МВ;  ОN=√2*CN. Или
2МВ=СN. Тогда 6МВ=2МВ+4МВ=2МВ+2CN = 2ВС.
AD=6MB+2BC (доказано выше).
AD=2BC+2BC==4ВС, что и требовалось доказать.