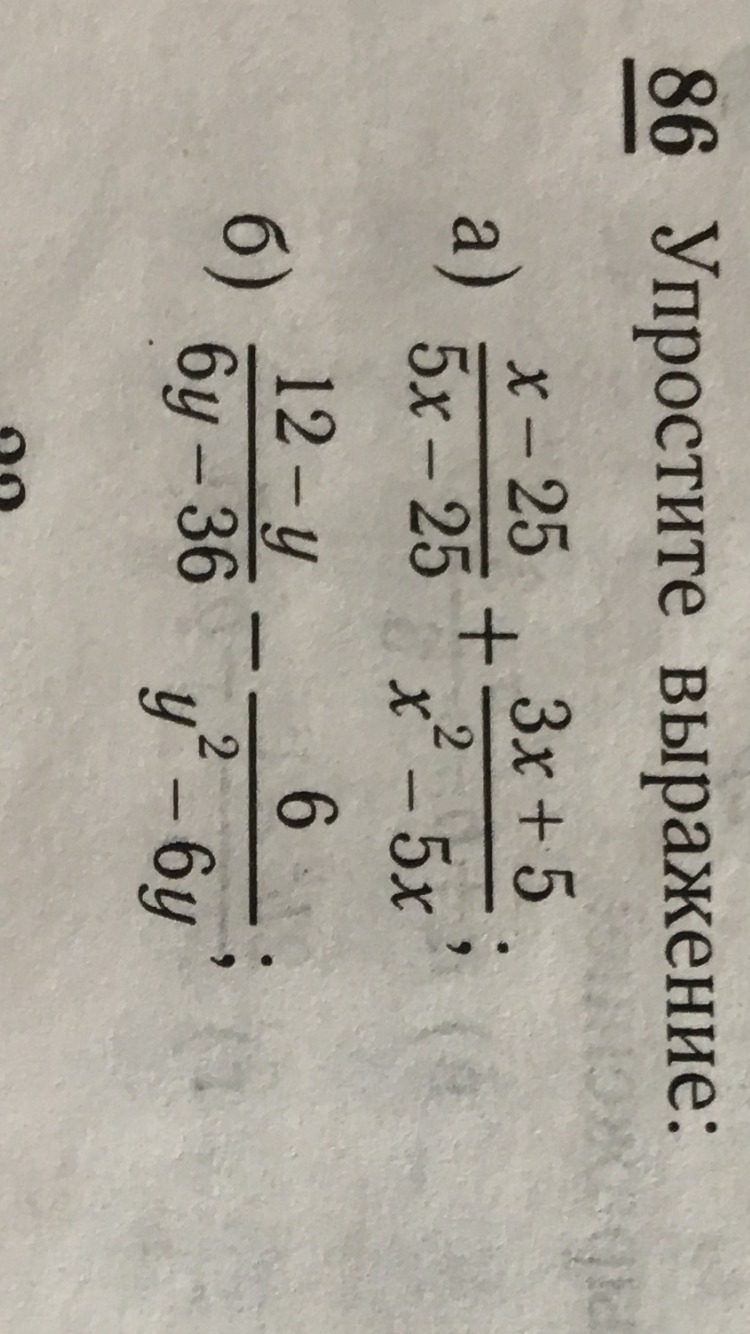Ответы
Ответ дал:
0
а) 
Разобьем знаменатели на множители:

Занесем под общий знаменатель 5x(x-5):

Свернем квадрат разности:

Полагая, что х не равен 5, сократим:

б)
Разобьем знаменатели на множители:

Занесем под общий знаменатель:

Свернем в квадрат разности:

Полагая, что у не равен 6, сократим:

Разобьем знаменатели на множители:
Занесем под общий знаменатель 5x(x-5):
Свернем квадрат разности:
Полагая, что х не равен 5, сократим:
б)
Разобьем знаменатели на множители:
Занесем под общий знаменатель:
Свернем в квадрат разности:
Полагая, что у не равен 6, сократим:
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад