Предмет: Алгебра
Автор: Ilyasssssss
Вопрос задан 2 года назад

Вычислить f'(1)+f'(4)
f(x)=|x^2-5x+4|

Denik777: Это бессмысленно, потому что производная у этой функции в точках 1 и 4 не существует.

Ilyasssssss: почему?

Denik777: По определению производной. В точке 1 левая производная равна -3, а правая равна 3. Они не равны, поэтому производная не существует.

Ilyasssssss: а почему они должны быть равными?

Ilyasssssss: все говорят разные вещи хотелось бы знать конкретное решение с конкретным ответом

Denik777: По определению производной производная функции в точке - это предел отношения приращений. Предел в точке существует только если предел слева равен пределу справа. А в данном случае они не равны

Ответы

Ответ дал: Denik777

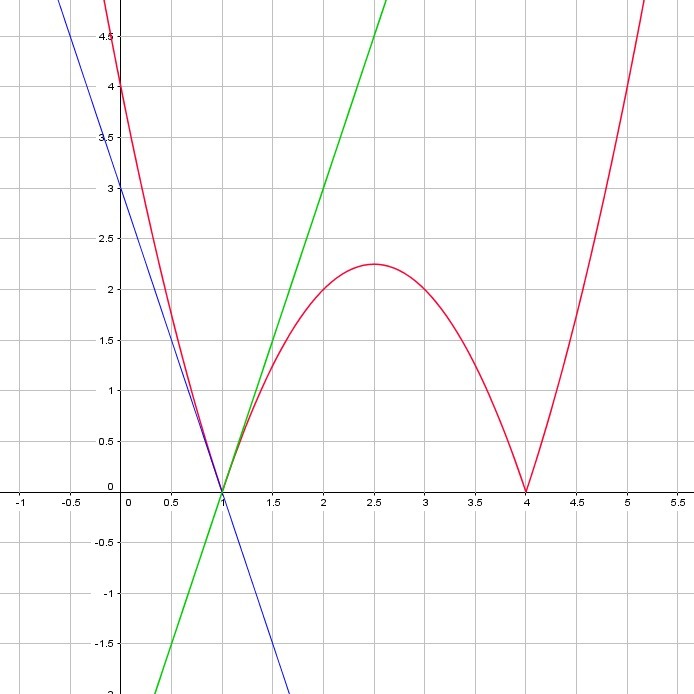
Доказательство прицеплено в первой картинке. Если нужно совсем наглядное объяснение, то оно во второй картинке с графиками: график функции f(x) (красная линия), в точке х=1 имеет "зубец" - что означает, что в этой точке есть две различных касательных к графику (синяя и зеленая прямые). А когда в какой-то точке график функции имеет не единственную касательную, то в этой точке функция не имеет производной. Аналогично, кстати и с точкой х=4.

Приложения: