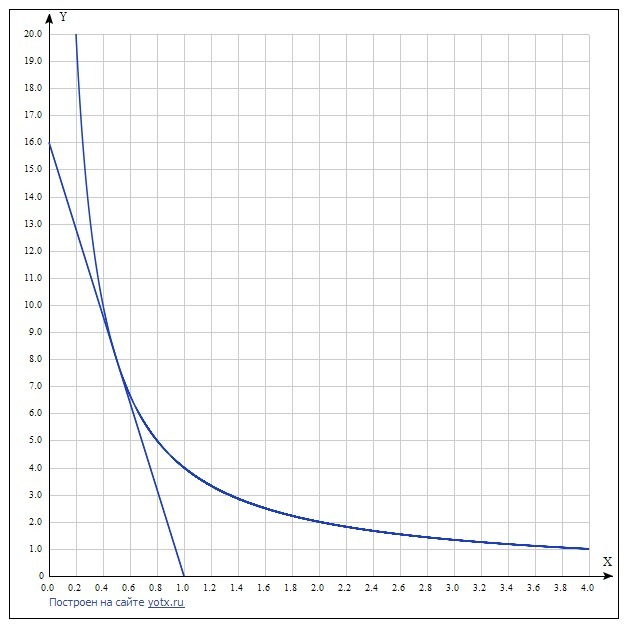
найдите площадь треугольника, ограниченного осями координат и касательной к графику y=4/x в точке с абсциссой х0 = 1/2
Ответы
Ответ дал:
0
Составляем уравнение касательной.
Точка касания: х=0,5, у = 4/0,5 = 8.
Производная y'= (4/x)' = (4'*x-4*x')/x²=-4/x².
Угловой коэффициент k=y'(0.5) = -4/0.25 = -16.
Уравнение касательной у-8 = -16*(х-0,5)
у=-16х+16.
Пересечение с осями х=0, у=16;
у=0, х=1. S=1/2 * a*h = 1/2 * 1*16 = 8.
Точка касания: х=0,5, у = 4/0,5 = 8.
Производная y'= (4/x)' = (4'*x-4*x')/x²=-4/x².
Угловой коэффициент k=y'(0.5) = -4/0.25 = -16.
Уравнение касательной у-8 = -16*(х-0,5)
у=-16х+16.
Пересечение с осями х=0, у=16;
у=0, х=1. S=1/2 * a*h = 1/2 * 1*16 = 8.
Приложения:
Вас заинтересует
1 год назад
2 года назад
3 года назад
3 года назад
8 лет назад