прямоугольная трапеция с основаниями 10 и 16 и высотой 8 вращают около меньшего основания, найти площадь поверхности тела вращения
Ответы
Ответ дал:
0
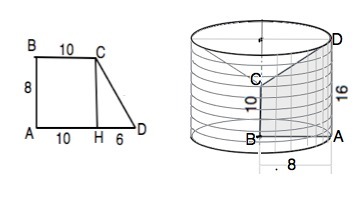
Тело вращения - цилиндр с радиусом основания, равным меньшей боковой стороне трапеции, с углублением в виде конуса того же радиуса.
Его площадь состоит из:
а) площади боковой поверхности конуса.
б) площади боковой поверхности цилиндра;
в) площади одного основания цилиндра.
Обозначим трапецию АВСD
а) S(бок.кон)=πrL
L– сторона CD трапеции. Высота трапеции СН "отсекает" от нее треугольник с катетами СН=АВ=8 и HD=AD-AH=16-10=6.
По т.Пифагора СD=10.
S(бок. конуса)=π•8•10=80π
б) S (бок. цил)=2π•r•h=2π•8•16=256π
в) S (осн)=πr²=π•8²=64π
S(полн)=π•(80+256+64)=400 π (ед. площади)
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад