Помогите найти область определения выражения
Приложения:
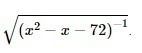
paradiseva:
где само задание?
В картинке)
Ответы
Ответ дал:
1
Приложения:

Не понятно написал
А почему область (-8;9) не входит?
Я поняла)
Вас заинтересует
1 год назад
1 год назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад