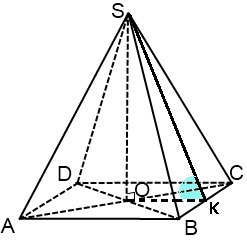
Диагональ основания правильной четырехугольной пирамиды равна 10 см, а угол между плоскостью боковой грани и плоскостью основания равен 45 градусов. Найдите площадь поверхности пирамиды.
Ответы
Ответ дал:
7
Sосн = d²/2 = 10² /2 = 50 см² - площадь основания
Тогда сторона основания: S=a² ⇒ a=√S = 5√2 см
Угол между высотами противоположной граней равен 180° -2·45° = 90°
Следовательно, см
см
Площадь боковой поверхности равен см²
см²
Площадь поверхности пирамиды
Sполн = Sосн + Sбок = см²
см²
Тогда сторона основания: S=a² ⇒ a=√S = 5√2 см
Угол между высотами противоположной граней равен 180° -2·45° = 90°
Следовательно,
Площадь боковой поверхности равен
Площадь поверхности пирамиды
Sполн = Sосн + Sбок =
Приложения:
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад