Точка P удалена от всех вершин равностороннего треугольника на 4 см.
Сторона треугольника равна 6 см,найдите расстояние от точки P до плоскости треугольника.
Ответы
Ответ дал:
0
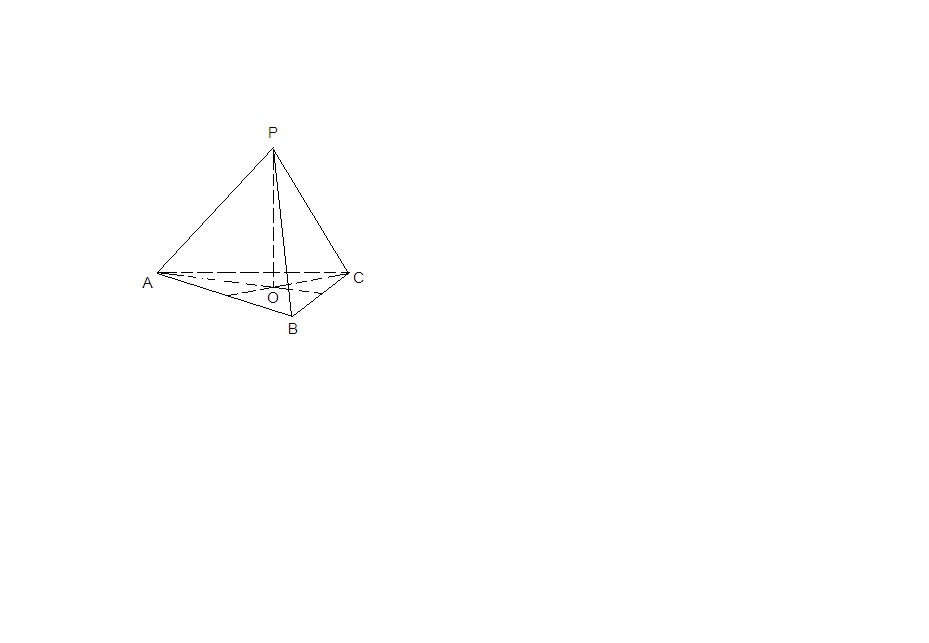
РА = РВ= РС = 4 см
Если равны наклонные, проведенные из одной точки, то равны и их проекции. Если РО⊥(АВС), то ОА = ОВ= ОС ⇒ О - центр окружности, описанной около треугольника. РО - искомое расстояние.
R = a√3/3, где а - сторона треугольника, R - радиус описанной окружности.
R = 6√3/3 = 2√3 см
ΔАОР: ∠О= 90°, по теореме Пифагора
PO = √(PA² - AO²) = √(16 - 12) = 2 см
Если равны наклонные, проведенные из одной точки, то равны и их проекции. Если РО⊥(АВС), то ОА = ОВ= ОС ⇒ О - центр окружности, описанной около треугольника. РО - искомое расстояние.
R = a√3/3, где а - сторона треугольника, R - радиус описанной окружности.
R = 6√3/3 = 2√3 см
ΔАОР: ∠О= 90°, по теореме Пифагора
PO = √(PA² - AO²) = √(16 - 12) = 2 см
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад