Question

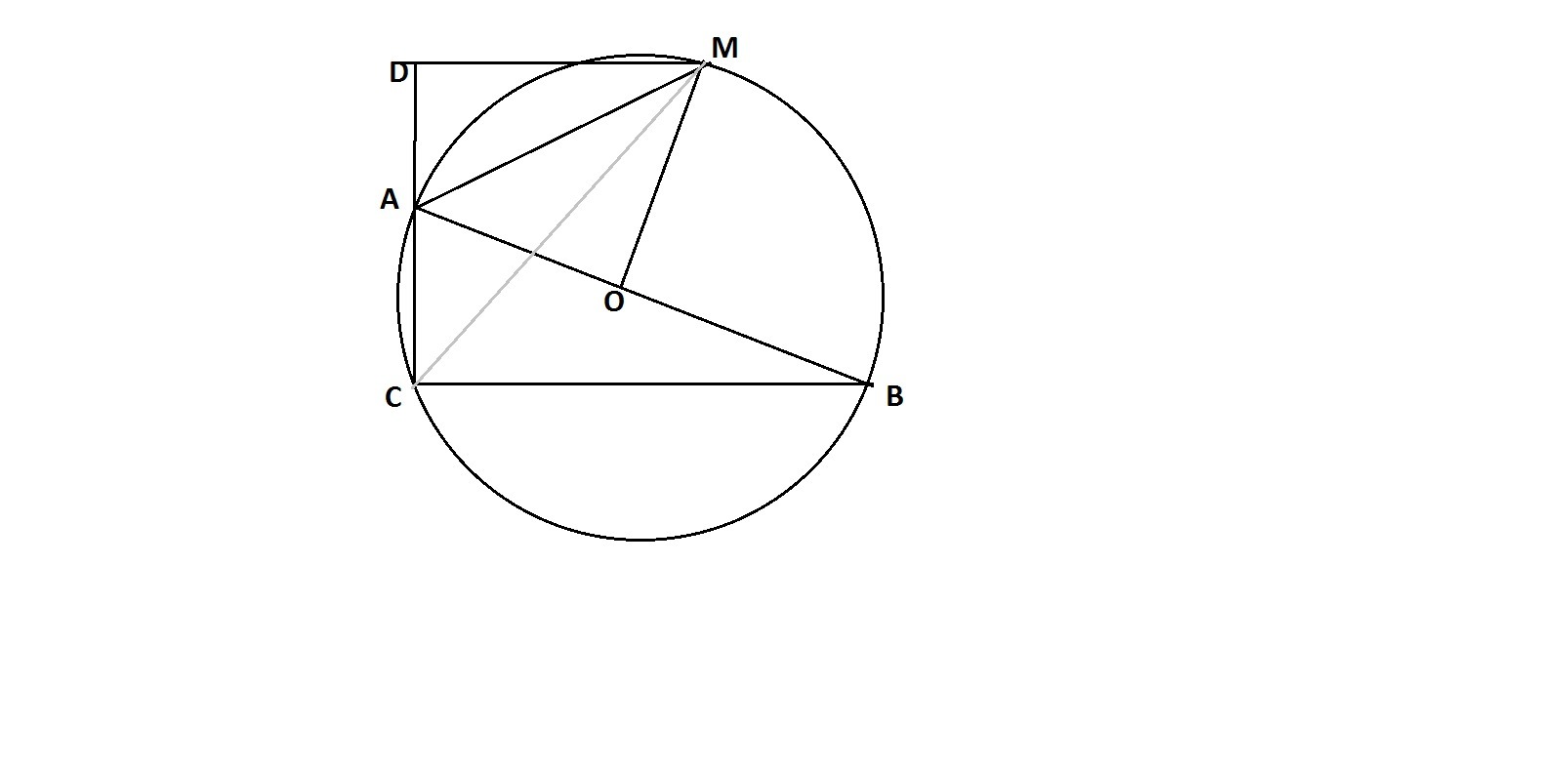
Прямоугольный треугольник ABC вписан в окружность.
Угол С прямой.
AC=1
BC=√3
Проведена хорда СM.
Угол САМ = 105 градусов.
Найти расстояние от M до прямой АС.

Answer 1

Найдём сначала угол данного вписанного треугольника.
$tgCAB = \dfrac{ \sqrt{3}} {1} = \sqrt{3} \\ arctgCAB = 60^{\circ}$
В прямоугольном треугольнике гипотенуза равна диаметру описанной окружности.
По теореме Пифагора:
$AB = \sqrt{AC^2 + BC^2} = \sqrt{3 + 1} = 2$
Тогда R = OA = OM = 1.
∠BAM = ∠CAM - ∠CAB = 105° - 60° = 45°.
Т.к. OA = OM = R и ∠BAM = 45°, то ΔOAM - равнобедренный и прямоугольный.
По теореме Пифагора:
$AM = \sqrt{OA^2 + OM^2} = \sqrt{1 + 1} = \sqrt{2}$
∠DAM = 180° - ∠CAM = 180° - 105° = 75°.
∠AMD = 90° - ∠DAM = 90° - 75° = 15°.
$cosAMD = cos15^{\circ} = \sqrt{\dfrac{1 + cos30^{\circ}}{2} } = \sqrt{\dfrac{1 + \dfrac{ \sqrt{3}} {2} }{2} } = \dfrac{ \sqrt{2 + \sqrt{3} }} {2} \\ \\ cosAMD = \dfrac{DM}{AM} \\ \\ \dfrac{ \sqrt{2 + \sqrt{3} }} {2} = \dfrac{DM}{ \sqrt{2} } \\ \\ \sqrt{4 + 2 \sqrt{3} } = 2DM \\ \\ DM = \dfrac{\sqrt{4 + 2 \sqrt{3} }}{2}$
Ответ: $DM = \dfrac{\sqrt{4 + 2 \sqrt{3} }}{2}.$