Question

В треугольнике ВКС проведена высота ВН, где точка Н на продолжении стороны КС за точку С. Известно, что сторона КС равна 11м, сторона ВС равна 15м, отрезок СН равен 9м. Найдите площадь треугольника ВКС.

Answer 1

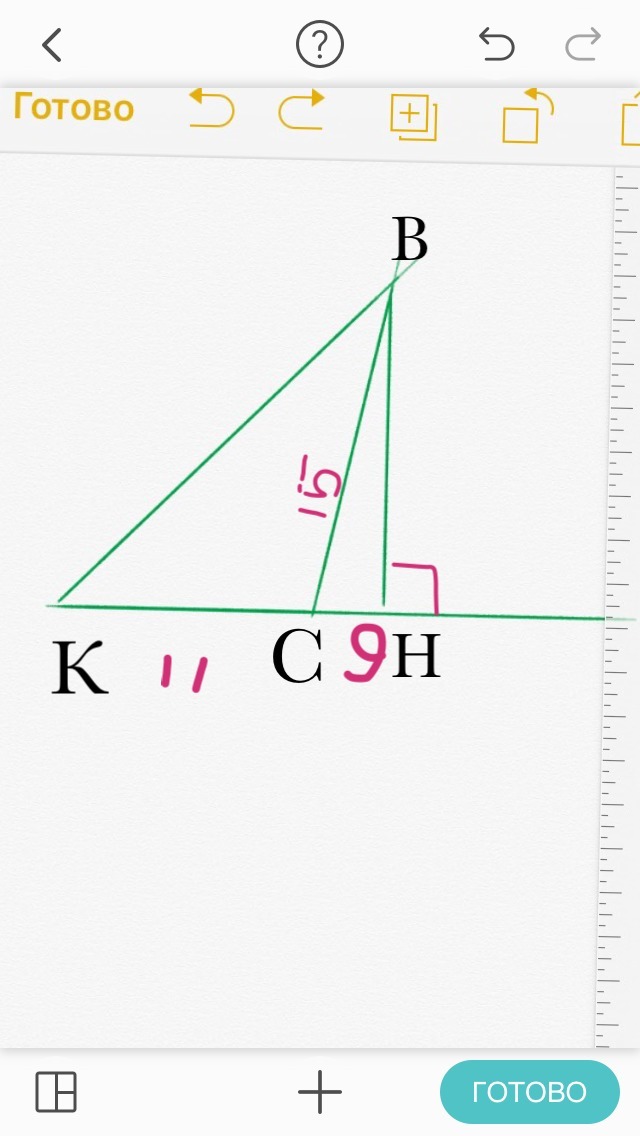
Начертим правильно рисунок.
Треугольник ВКС.
Высота ВН лежит вне треугольника.
Точка Н находится на продолжении стороны КС.

Отмечаем на рисунке ВС=15
СН=9
КС=11

ВН-высота, следовательно, треугольник ВНС - прямоугольный.
Нам известны гипотенуза 15 и катет 9.
По теореме Пифагора
ВН=корень из (225-81)= 12

Рассмотрим треугольник ВКС.
Площадь = высота*основание*0,5=ВН*КС*0,5=12*11*0,5=66.
Ответ: 66