Question

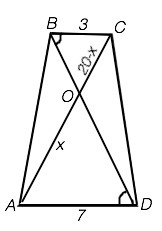
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O , BC=3 , AD=7 , AC=20 . Найдите AO .

Answer 1

Диагонали трапеции при пересечении образуют с её основаниями  треугольники, в которых углы при точке пересечения равны как вертикальные, углы при основаниях - как накрестлежащие. =>

∆ ВОС~∆ AOD по двум углам. 

Примем АО = х, тогда ОС=20-х

Из подобия ∆ АОD и ∆ ВОС следует отношение

ОС:АО=ВС:AD

(20-х):х.=3:7 =>

3х=140-7х

10х=140

х=14

АО=14  (ед. длины)