Question

При каком наибольшем значении параметра а система уравнений
имеет ровно три различных решения?

x^2+(y-1)^2=1
y=|x-a|

Answer 1

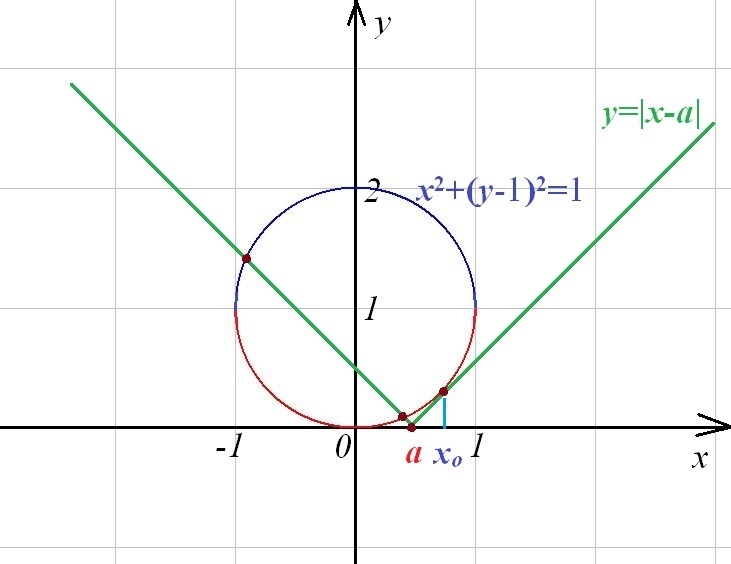
На моем рисунке показана ситуация, при которой данная система уравнений имеет ровно три решения.
Задача сводится к нахождению наибольшего положительного значения а, при котором левая "ветвь" графика модуля пересекает окружность в двух точках , а правая - касается окружности. в некоторой точке х0.
Красная дуга окружности имеет формулу $y=1-\sqrt{1-x^2},\ -1 \leq x \leq 1$.
Найдем точку касания (х0) прямой у=x-a и окружности.
$k=f'(x_o)=1\\ f'(x)=(1- \sqrt{1-x^2} )'=- \dfrac{-2x}{2\sqrt{1-x^2} } =\dfrac{x}{\sqrt{1-x^2} } \\ \dfrac{x}{\sqrt{1-x^2} } =1\\ \sqrt{1-x^2}=x\\ 1-x^2=x^2\\ x^2= \frac{1}{2}\\ x=\б \sqrt{ \frac{1}{2} }= \б \frac{ \sqrt{2} }{2}$
В нашем случае х0>0 ⇒ $x_0= \frac{ \sqrt{2} }{2}$
Составим уравнение касательной к окружности в точке $x_0= \frac{ \sqrt{2} }{2}$
$y=f'(x_0)(x-x_0)+f(x_0)\\ f(x_0)=f( \frac{ \sqrt{2} }{2} )=1- \sqrt{1- \frac{1}{2} } =1-\sqrt{\frac{1}{2} } =1- \frac{ \sqrt{2} }{2} \\ y=1*(x-\frac{ \sqrt{2} }{2})+1-\frac{ \sqrt{2} }{2}\\ y=x+1- \sqrt{2}$
Абсцисса точки пересечения касательной $y=x+1- \sqrt{2}$ и окружности и является искомым значением параметра а:
$0=x+1- \sqrt{2} \\ a=x=\sqrt{2}-1$
Ответ: $a=\sqrt{2}-1$