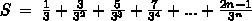Ответы
Ответ дал:
1
представим члены суммы в виде разности:


становится очевидно, что сократятся все слагаемые суммы, кроме и последнего слагаемого
и последнего слагаемого  ⇒
⇒

становится очевидно, что сократятся все слагаемые суммы, кроме
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад