
Очень интересная задача попалась, пожалуйста, с объяснением. Решается просто, но не торопитесь давать ответ! 11 класс, задача повышенной сложности.
Аноним:
Не представляю где применимы такие логарифмы.
число e знаете? )
Ну, оно иррациональное. Я говорил, если что, не про натуральные логарифмы, а про те, что в этом вопросе.
почитайте про Джона Непера :)
который их и придумал
вот там узнаете как раз, для чего они предназначены
ничего из того, что есть, не появилось просто так
Ладно, спасибо Вам :)
Хотя всё-же не представляю где применимы логарифмы с переменными в основании и подлогарифмическим выражением с переменной.
математике свойственно всё обобщать
Ответы
Ответ дал:
1
log(x^-1, (2x-1)/(x-1))<=-1
-log(x, (2x-1)/(x-1))<=-1
log(x, (2x-1)/(x-1))=>1
(2x-1)/(x-1)>0
x ∈ (-∞; 0.5) ∪ (1; +∞)
log(x, (2x-1)/(x-1))=>log(x, x)
x>1
(2x-1)/(x-1)=>x
(2x-1-x^2+x)/(x-1)=>0
(x^2-3x+1)/(x-1)<=0
((x-(3-sqrt(5))/2)(x-(3+sqrt(5))/2))/(x-1)<=0
x ∈ (1; (3+sqrt(5))/2]
x<1
(2x-1)/(x-1)<=x
(2x-1-x^2+x)/(x-1)<=0
(x^2-3x+1)/(x-1)=>0
((x-(3-sqrt(5))/2)(x-(3+sqrt(5))/2))/(x-1)=>0
x ∈ [(3-sqrt(5))/2; 0.5)
x ∈ [(3-sqrt(5))/2; 0.5) ∪ (1; (3+sqrt(5))/2]
-log(x, (2x-1)/(x-1))<=-1
log(x, (2x-1)/(x-1))=>1
(2x-1)/(x-1)>0
x ∈ (-∞; 0.5) ∪ (1; +∞)
log(x, (2x-1)/(x-1))=>log(x, x)
x>1
(2x-1)/(x-1)=>x
(2x-1-x^2+x)/(x-1)=>0
(x^2-3x+1)/(x-1)<=0
((x-(3-sqrt(5))/2)(x-(3+sqrt(5))/2))/(x-1)<=0
x ∈ (1; (3+sqrt(5))/2]
x<1
(2x-1)/(x-1)<=x
(2x-1-x^2+x)/(x-1)<=0
(x^2-3x+1)/(x-1)=>0
((x-(3-sqrt(5))/2)(x-(3+sqrt(5))/2))/(x-1)=>0
x ∈ [(3-sqrt(5))/2; 0.5)
x ∈ [(3-sqrt(5))/2; 0.5) ∪ (1; (3+sqrt(5))/2]
Ответ дал:
2
Решение задания приложено.
Приложения:
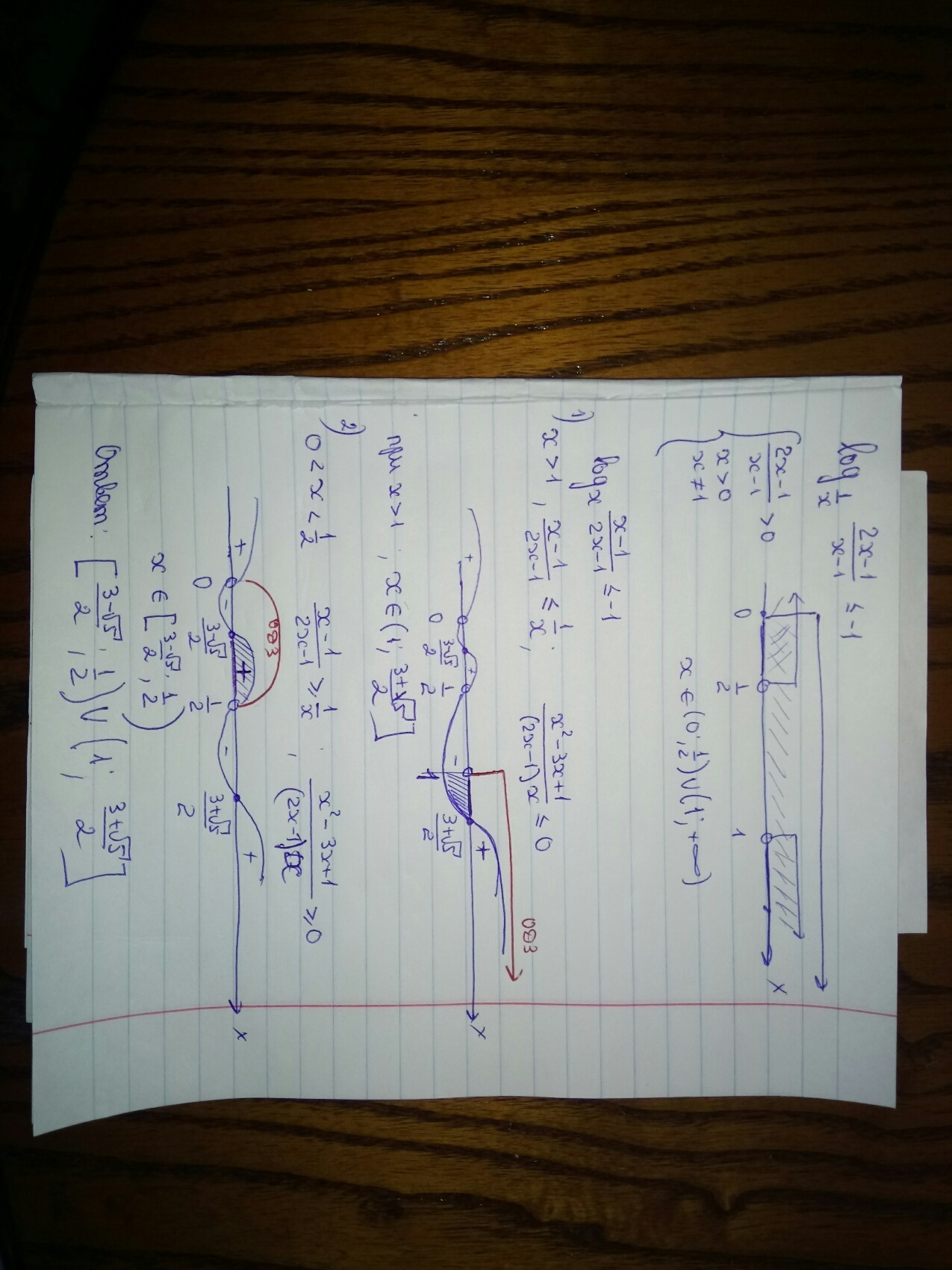
Спасибо.
Вас заинтересует
1 год назад
1 год назад
3 года назад
9 лет назад
9 лет назад