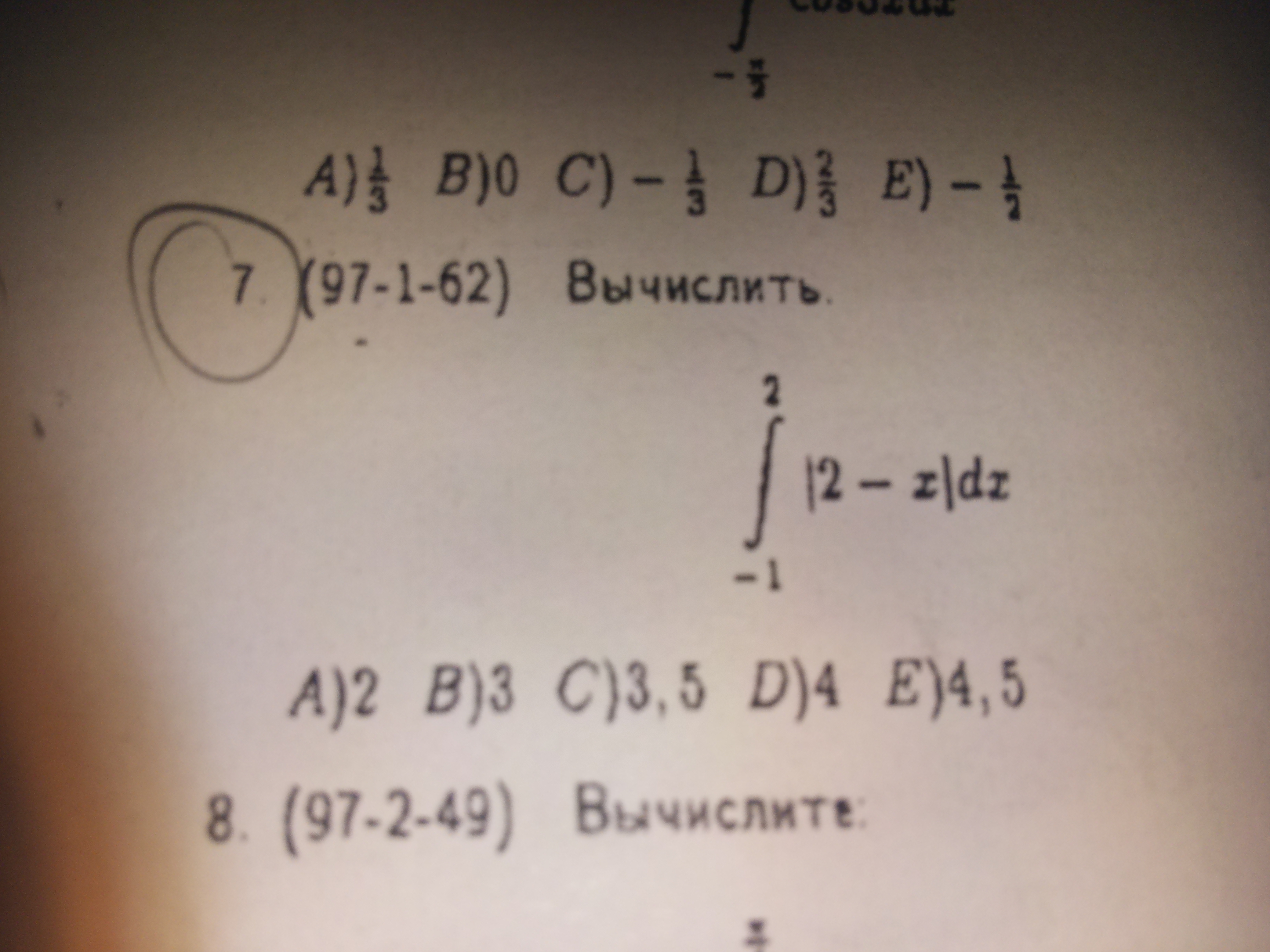Ответы
Ответ дал:
1
2
∫ |2 - x| dx
-1
Раскроем модуль:
|2 - x| = -(2 - x), если 2 - x ≤ 0, или x ≥ 2
|2 - x| = 2 - x, если 2 - x ≥ 0, или x ≤2
Отсюда видно, что пределы интегрирования полностью укладываются в интервал x ≤ 2. Поэтому для вычисления определённого интеграла берётся именно это раскрытие. Если бы интервал интегрирования перехлёстывался, попадая сразу на два, то пределы интегрирования пришлось бы разбить с учётом раскрытия модуля.
А так, наш модуль в интерваля от (-1) до (+2) равен: |2 - x| = 2 - x
2 2
∫ (2 - x) dx = (2x - x^2 /2) | = (2*2 - 2^2 /2) - (2*(-1) - (-1)^2 /2) =
-1 -1
= (4 - 2) - (-2 - 1/2) = 2 + 2 + 1/2 = 4.5
∫ |2 - x| dx
-1
Раскроем модуль:
|2 - x| = -(2 - x), если 2 - x ≤ 0, или x ≥ 2
|2 - x| = 2 - x, если 2 - x ≥ 0, или x ≤2
Отсюда видно, что пределы интегрирования полностью укладываются в интервал x ≤ 2. Поэтому для вычисления определённого интеграла берётся именно это раскрытие. Если бы интервал интегрирования перехлёстывался, попадая сразу на два, то пределы интегрирования пришлось бы разбить с учётом раскрытия модуля.
А так, наш модуль в интерваля от (-1) до (+2) равен: |2 - x| = 2 - x
2 2
∫ (2 - x) dx = (2x - x^2 /2) | = (2*2 - 2^2 /2) - (2*(-1) - (-1)^2 /2) =
-1 -1
= (4 - 2) - (-2 - 1/2) = 2 + 2 + 1/2 = 4.5
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад