Question

Боковое ребро правильной четырехугольной пирамиды равно 2 см и наклонено к плоскости основания под углом 60 градусов, найдите объем пирамиды

Answer 1

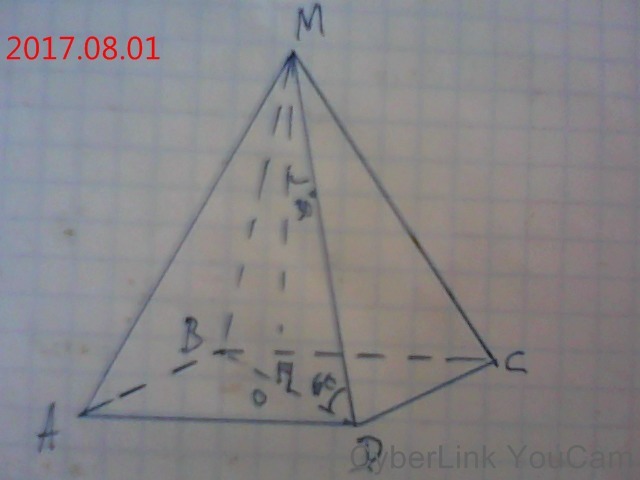
ΔОМD. МD=2 см; ∠МDО=60°; ∠ОМD=30°; ОD=0,5МD=1 см.
ОМ²=МD²-ОD²=4-1=3;  ОМ=√3 см.
ΔВМD. ВD=ОВ+ОD=1+1=2 см.
АВСD - квадрат, сторона которого равна √2 см;
площадь равна S=√2²=2 см².
V=(2·√3)/3=2√3 /3 см³.