Ответы
Ответ дал:
1
Решение дано на фото.
Приложения:
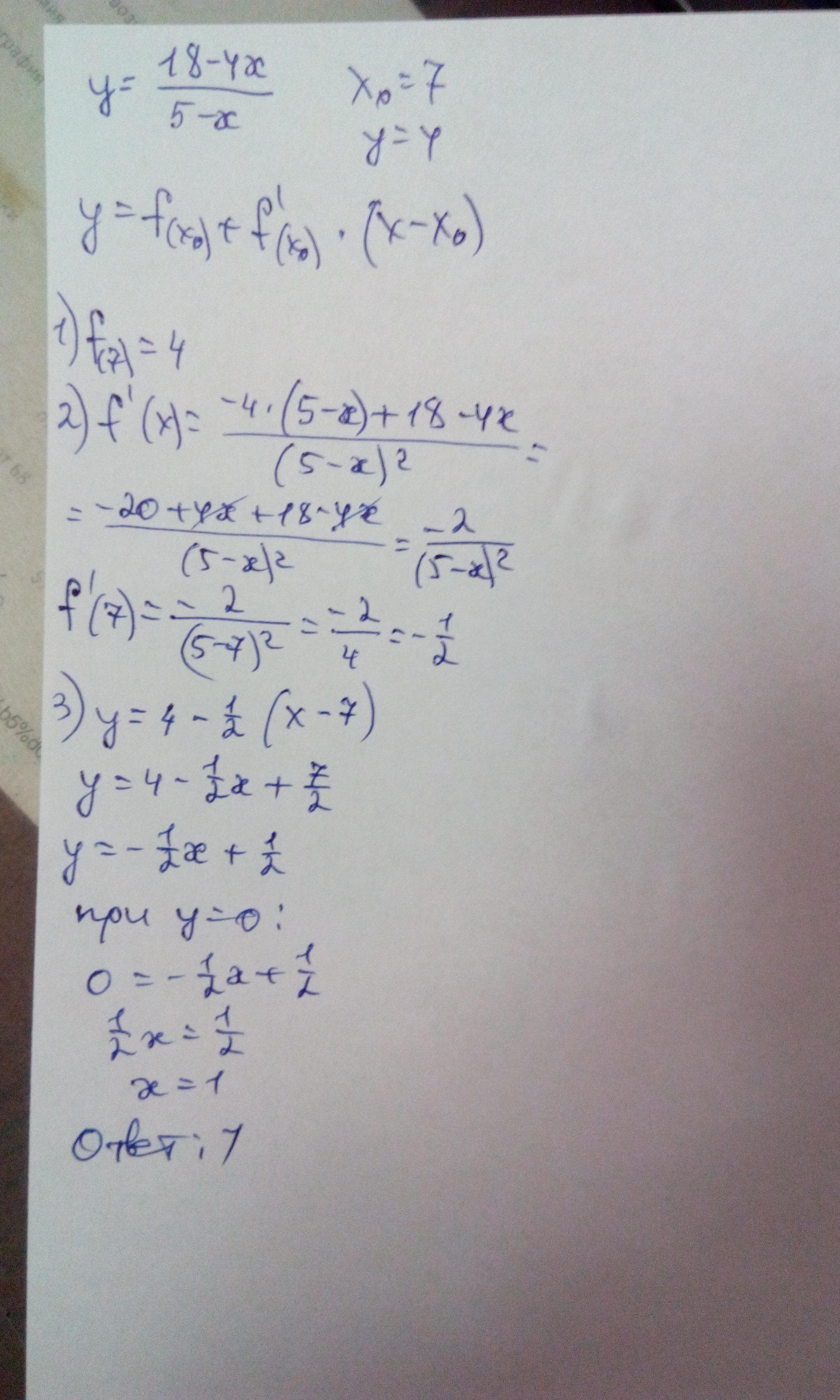
Lantica:
как вы провели второе действие?
Решение неверное! Точка (7; 4) не лежит на кривой!!! А точка касания (Хо) не известна!!!
Ответ дал:
3
Производная заданной функции равна: y' = -2/(5-x)².
Здесь х - ордината точки касания.
Уравнение касательной вида у = кх + в.
В этом уравнении коэффициент к равен производной.
Коэффициент в равен: в = у - кх.
Из условия, что касательная проходит через точку (7; 4) получаем:
в = 4 - 7к.
Тогда уравнение касательной: у = кх + 4 - 7к = к(х - 7) + 4.
Подставим вместо к его выражение через производную и приравняем уравнение касательной и функции - ведь в точке касания они равны.

Приведём к общему знаменателю и приравняем числители:

4x = 24.
x = 24/4 = 6. Это абсцисса точки касания - Хо = 6.
Уо = (18-4*6)/(5-6) = -6/-1 = 6.
Отсюда находим коэффициент к как тангенс угла наклона касательной:
к = Δу/Δх = (6-4)/(6-7) = 2/-1 = -2.
Коэффициент в = 4 - 7*(-2)= 4 + 14 = 18.
Получили уравнение касательной:
у = -2х + 18.
Искомую абсциссу точки пересечения с осью ОХ касательной к кривой проходящей через точку (7,4) находим их этого уравнения при у = 0.
-2х + 18 = 0,
х = 18/2 = 9.
Здесь х - ордината точки касания.
Уравнение касательной вида у = кх + в.
В этом уравнении коэффициент к равен производной.
Коэффициент в равен: в = у - кх.
Из условия, что касательная проходит через точку (7; 4) получаем:
в = 4 - 7к.
Тогда уравнение касательной: у = кх + 4 - 7к = к(х - 7) + 4.
Подставим вместо к его выражение через производную и приравняем уравнение касательной и функции - ведь в точке касания они равны.
Приведём к общему знаменателю и приравняем числители:
4x = 24.
x = 24/4 = 6. Это абсцисса точки касания - Хо = 6.
Уо = (18-4*6)/(5-6) = -6/-1 = 6.
Отсюда находим коэффициент к как тангенс угла наклона касательной:
к = Δу/Δх = (6-4)/(6-7) = 2/-1 = -2.
Коэффициент в = 4 - 7*(-2)= 4 + 14 = 18.
Получили уравнение касательной:
у = -2х + 18.
Искомую абсциссу точки пересечения с осью ОХ касательной к кривой проходящей через точку (7,4) находим их этого уравнения при у = 0.
-2х + 18 = 0,
х = 18/2 = 9.
Приложения:
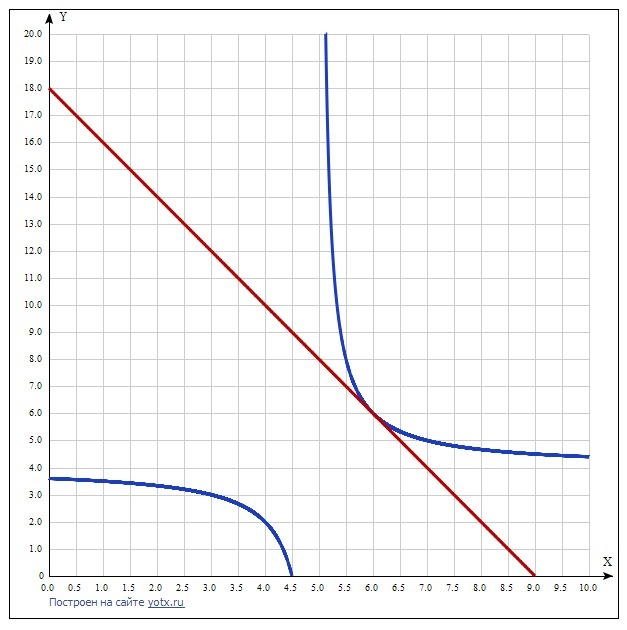
Вас заинтересует
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад