Question

Докажите,что любые две медианы треугольника в точке пересечения делятся в отношении 2:1

Answer 1

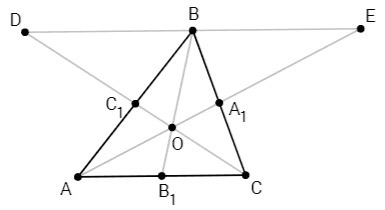
AA₁, BB₁, CC₁ - чевианы, проходящие через одну точку.

DE||AC

△DOE~△AOC => BO/OB₁ =DE/AC =DB/AC +BE/AC
△DC₁B~△AC₁C => DB/AC=BC₁/C₁A
△BA₁E~△AA₁C => BE/AC=BA₁/A₁C

BO/OB₁= BC₁/C₁A +BA₁/A₁C

Если BC₁=C₁A и BA₁=A₁C, то BO/OB₁ =2

Answer 2

BO/OB1 = сумме пропорций двух сторон? Я разобрался в вашем решении,но этот момент не понял. То есть это такая формула? Она всегда действует да? Прошу прощения ,если для вас этот вопрос покажется глупым ,как и я,но я хочу разобраться. Заранее благодарен

Answer 3

На самом деле есть замечательная формула Ван-Обеля, которая это и утверждает

Answer 4

Ух ты! Я не знал... А вы не подскажите хорошую книгу или учебник,где есть эта теорема и задачи по ней? Буду очень признателен! Она только для треугольника с медианами применима ?

Answer 5

Она применима для любых отрезков AA_1, BB_1, CC_1, пересекающихся водной точке. Для медиан она сразу дает нужный ответ 2:1, для биссектрис "сумма прилежащих сторон к противолежащей" и т.д. Есть в книжке Понарина

Answer 6

Благодарствую!