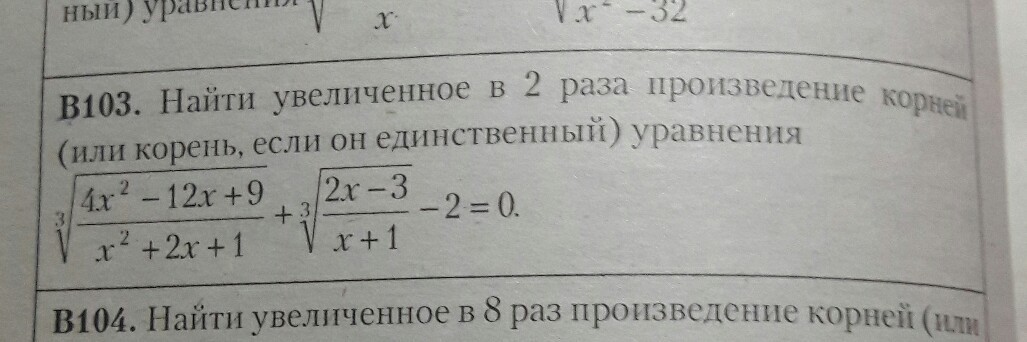Question

В103, помогите пожалуйста

Answer 1

∛[(2x-3)/(x+1)]²+∛[(2x-3)/(x+1)-2=0
∛[(2x-3)/(x+1)=t
t²+t-2=0
Если в уравнении ax²+bx+c=0, a+b+c=0⇒x1=1 U x2=c/a⇒
t1=1⇒∛[(2x-3)/(x+1)=1
(2x-3)/(x+1)=1
2x-3=x+1
2x-x=1+3
x=4
t2=-2⇒∛[(2x-3)/(x+1)=-2
(2x-3)/(x+1)=-8
2x-3=-8x-8
2x+8x=-8+3
10x=-5
x=-0,5
Удвоенное произведение корней равно 2*(-0,5)*4=-4

Answer 2

Замечания: 1) Вы используете букву a в двух смыслах - как неизвестную и как старший коэффициент. Так нельзя. 2) Странная логика: x2=c/a следовательно a=1. 3) Вы не сосчитали то, что требовал автор

Answer 3

По поводу 2) соглашусь, тактически не понятно