Ответы
Ответ дал:
0
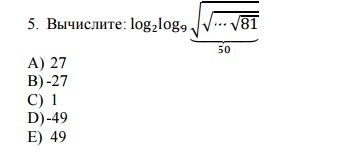
Используем следующие свойства:
![sqrt[n]{x} = x ^{frac{1}{n} }\ \
sqrt{ sqrt{x} } = x^{ frac{1}{4} } \ \
sqrt{ sqrt{... sqrt{x} } } = x^{ dfrac{1}{2^{50}}} \ \
log_{a}a = 1 \ \
log_{a}a^r = r \ \
a^{-n} = dfrac{1}{a^{n}} sqrt[n]{x} = x ^{frac{1}{n} }\ \
sqrt{ sqrt{x} } = x^{ frac{1}{4} } \ \
sqrt{ sqrt{... sqrt{x} } } = x^{ dfrac{1}{2^{50}}} \ \
log_{a}a = 1 \ \
log_{a}a^r = r \ \
a^{-n} = dfrac{1}{a^{n}}](https://tex.z-dn.net/?f=+sqrt%5Bn%5D%7Bx%7D+%3D+x+%5E%7Bfrac%7B1%7D%7Bn%7D+%7D%5C+%5C+%0A+sqrt%7B+sqrt%7Bx%7D+%7D+%3D++x%5E%7B+frac%7B1%7D%7B4%7D+%7D+%5C+%5C+%0A+sqrt%7B+sqrt%7B...+sqrt%7Bx%7D+%7D+%7D+%3D+x%5E%7B+dfrac%7B1%7D%7B2%5E%7B50%7D%7D%7D+%5C+%5C+%0Alog_%7Ba%7Da+%3D+1+%5C+%5C+%0Alog_%7Ba%7Da%5Er+%3D+r+%5C+%5C+%0Aa%5E%7B-n%7D+%3D++dfrac%7B1%7D%7Ba%5E%7Bn%7D%7D+)

Ответ: D.
Ответ: D.
Ответ дал:
0
можешь объяснить по точнее. Где корень и т.д
Ответ дал:
0
Квадратный корень - это степень 1/2, два подряд идущих квадратных корня - это 1/2*1/2 = 1/4 степень, 50 подряд идущих квадратных корней - это степень 1/2^{50}
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад