Question

Найти площадь закрашенной фигуры, с объяснением, пожалуйста.

Answer 1

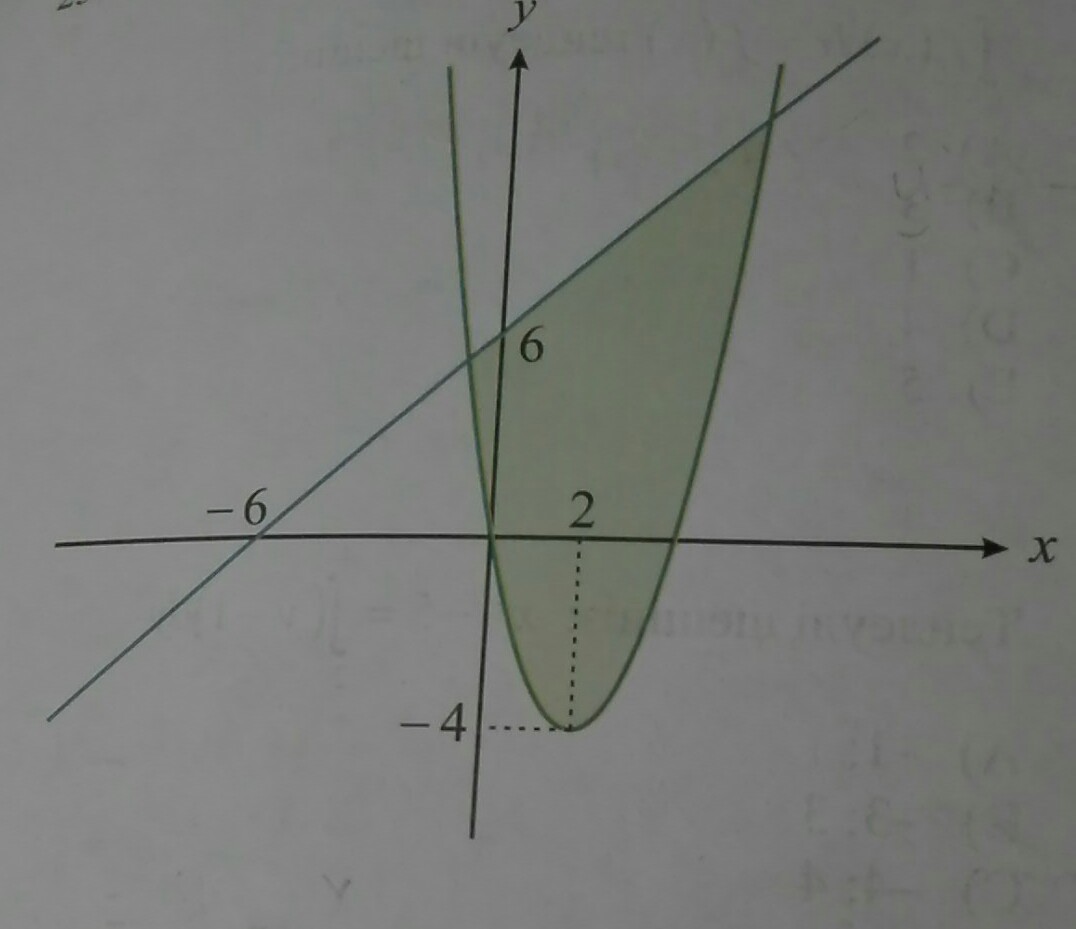
Выведем уравнения прямой и параболы.
Уравнение прямой задаётся в виде y = kx + m
Прямая проходит через точки (-6; 0) и (0; 6) 
0 = -6k + m
6 = 0k + m

6k = m
m = 6

k = 1
m = 6 ⇒ y = x + 6

Уравнение параболы можно задать в виде y = ax² + bx + c.
Парабола проходит через точки (0; 0); (2; -4); (4; 0) (вершиной будет точка (2; -4), прямая x = 2 - ось симметрии данной параболы, поэтому точка (0; 0) симметрична точке (4; 0) относительно оси x = 2).
Подставляем координаты:
-4 = 4a + 2b + c
0 = 16a + 4b + c
0 = 0 + 0 + c

c = 0
16a = -4b
2a + b = -2

c = 0
b = -4a
2a - 4a = -2

c = 0
b = -4a
-2a = -2

c = 0
a = 1
b = -4 ⇒ y = x² - 4x 


Найдём точки пересечения прямой и параболы:
x² - 4x = x + 6 
x² - 5x - 6 = 0 
x₁ + x₂ = 5
x₁x₂ = -6
x₁ = 6; x₂ = -1
x = -1 - нижний предел, x = 6 - верхний предел интегрирования:

$intlimits^{6}_{-1} {(x + 6 - x^2 + 4x)} , dx = intlimits^{6}_{-1} {(-x^2 + 5x + 6 )} , dx = \ \ bigg (-dfrac{x^3}{3} + dfrac{5x^2}{2} + 6x bigg ) bigg |^{6}_{-1} = -dfrac{1}{3} (6^3 + 1) + 2,5(36 - 1) + 6(6 + 1) = \ \ -dfrac{217}{3} + dfrac{175}{2} + 42 = dfrac{252 + 525 - 434}{6} = dfrac{343}{6} = 57 dfrac{1}{6}$

Answer 2

внизу только у меня галимотья?

Answer 3

самое интересное и не понять

Answer 4

так я и думала-спасибо!

Answer 5

на рисунке изображена парабола, смещенная по иксу на 2 и по игреку на -4, значит она задается функцией: 
у=(x-2)²-4

прямая задается функцией:
y=kx+b, где k=tga
tga=6/6=1, то есть k=1
Так как прямая поднята вверх на 6 единиц, значит b=6

прямая задана функцией
у=х+6

теперь находим их точки пересечения:
$(x-2)^2-4=x+6 \ x^2-4x+4-4=x+6 \ x^2-5x-6=0 \ x_1=6 \ x_2=-1$

Значит вся закрашенная область находится в промежутке от -1 до 6
составляем интеграл (верхняя функция минус нижняя)

 
$intlimits^6_{-1} {[x+6-((x-2)^2-4)]} , dx = intlimits^6_{-1} {[x+6-(x^2-4x)]} , dx = \ \ = intlimits^6_{-1} {(x+6-x^2+4x)} , dx = intlimits^6_{-1} {(6+5x-x^2)} , dx =6x+ frac{5x^2}{2} - frac{x^3}{3} |_{-1} ^6\ \ =(6*6+ frac{5*6^2}{2} - frac{6^3}{3} )-(6*(-1)+ frac{5*(-1)^2}{2} - frac{(-1)^3}{3} )=54+6- frac{5}{2}- frac{1}{3} \ \ \ = frac{343}{6}\ \ OTBET: frac{343}{6}$