Question

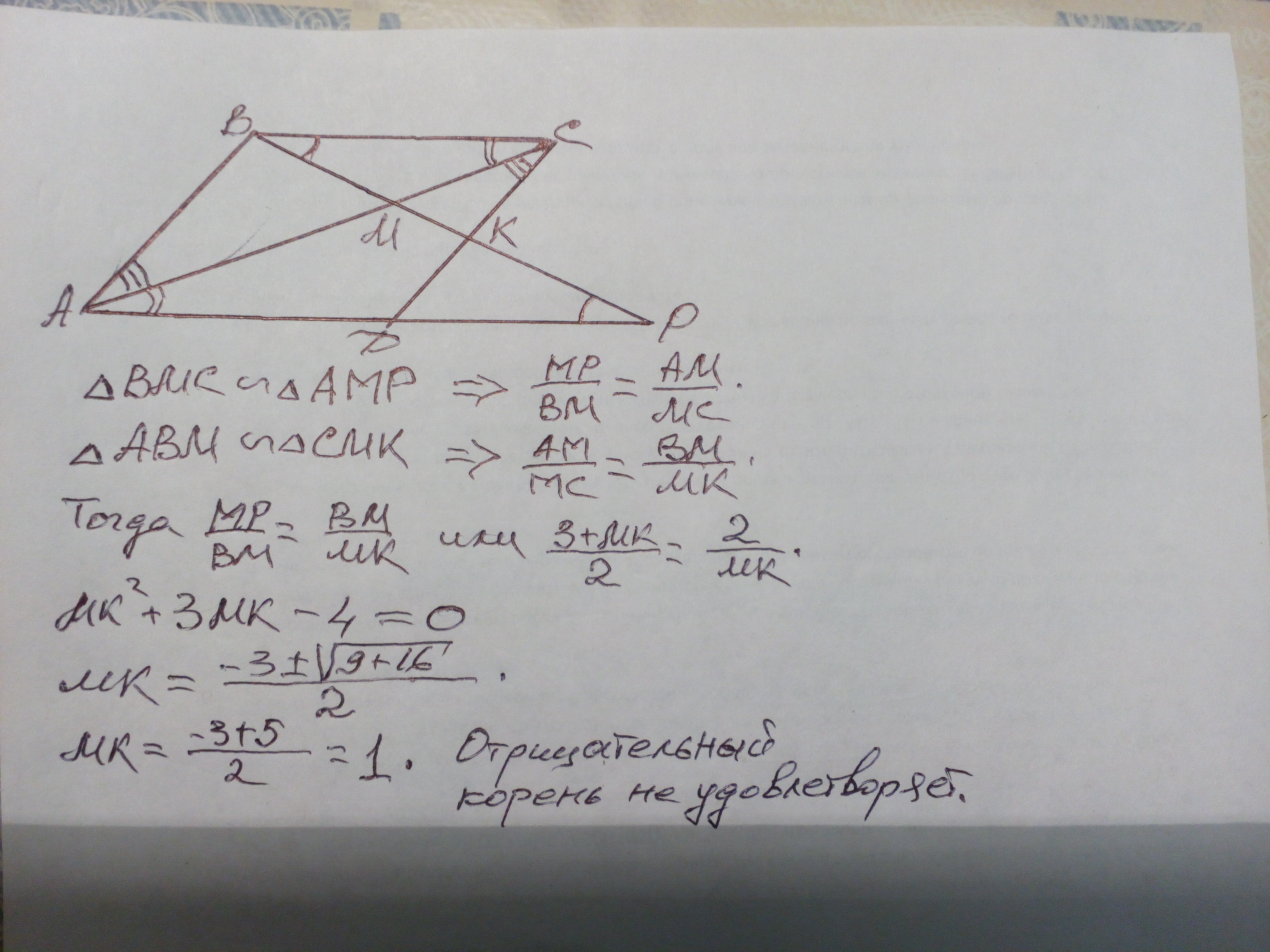
Точка K лежит на стороне CD параллелограмма ABCD. Прямая BK пересекает диагональ AC в точке M, а продолжение стороны AD в точке P. Известно, что BM=2 и KP=3. Найти длину отрезка MK.

Answer 1

Треугольник ВМС подобен треугольнику АМР по двум углам
 (<ВМС=<АМР как вертикальные, <ВСА=<САР как накрест лежащие при параллельных ВС и АР и секущей АС). Из подобия имеем:
МР/ВМ=АМ/МС. (1)
Треугольник АВС подобен треугольнику СМК по двум углам
(<АМВ=<СМК как вертикальные, <ВАМ=<АСК как накрест лежащие при параллельных АВ и CD и секущей АС). Из подобия имеем:
АМ/МС=ВМ/МК. (2).
Приравняем (1) и (2). Тогда 
МР/ВМ=ВМ/МК или (3+МК)/2=2/МК. Отсюда
МК^2+3МК-4=0. Решаем квадратное уравнение.
МК=(-3+√(9+16))/2=1.
Отрицательное значение корня не удовлетворяет условию.
Ответ: МК=1.