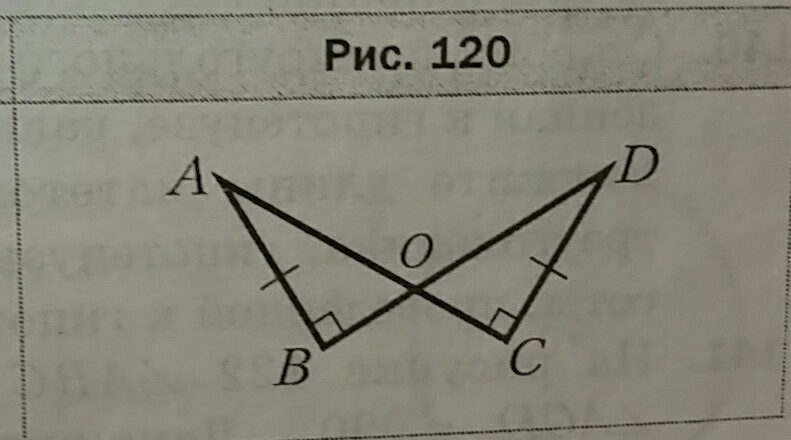
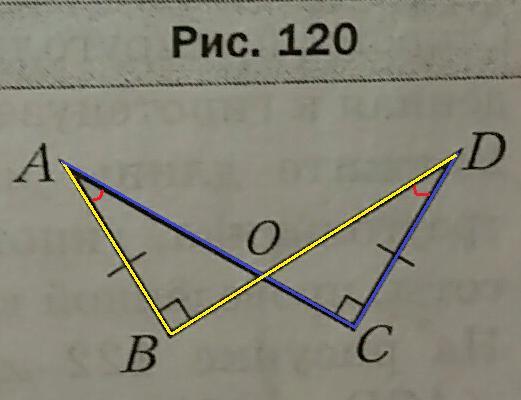
На рисунке 120 ∠ABO = ∠DCO = 90°, AB = CD. Найдите AO, если DO = 11см.
С подробным решением, пожалуйста.
Приложения:
Ответы
Ответ дал:
36
В ΔABO и ΔDCO:
Один угол прямой (∠ABO = 90° = ∠DCO), поэтому треугольники являются прямоугольными. Острый угол прямоугольного треугольника меньше 90°, поэтому сумма двух острых углов прям. тр. будет меньше 180°.
Стороны ∠BAO соответственное перпендикулярны сторонами ∠CDO (AB⊥DO и AO⊥DC), тогда ∠BAO и ∠CDO в сумме дают 180°, либо равны. Выше мы рассмотрели, что они не могут давать в сумме 180°, поэтому они равны.
∠BAO = ∠CDO
Прямоугольные треугольники ABO и DCO равны по катету (AB=DC) и прилежащему углу (∠BAO=∠CDO), откуда следует равенство их гипотенуз: AO = DO.
DO = 11см ⇒ AO = 11см.
Ответ: 11см.
Приложения:
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад