с пунктов А и В одновременно вышли два пешехода и встретились через 2 часа. найдите скорость каждого из пешеходов, если один из них прибыл в пункт А на 54 минуты раньше, чем второй пешеход в пункт В
Ответы
Ответ дал:
0
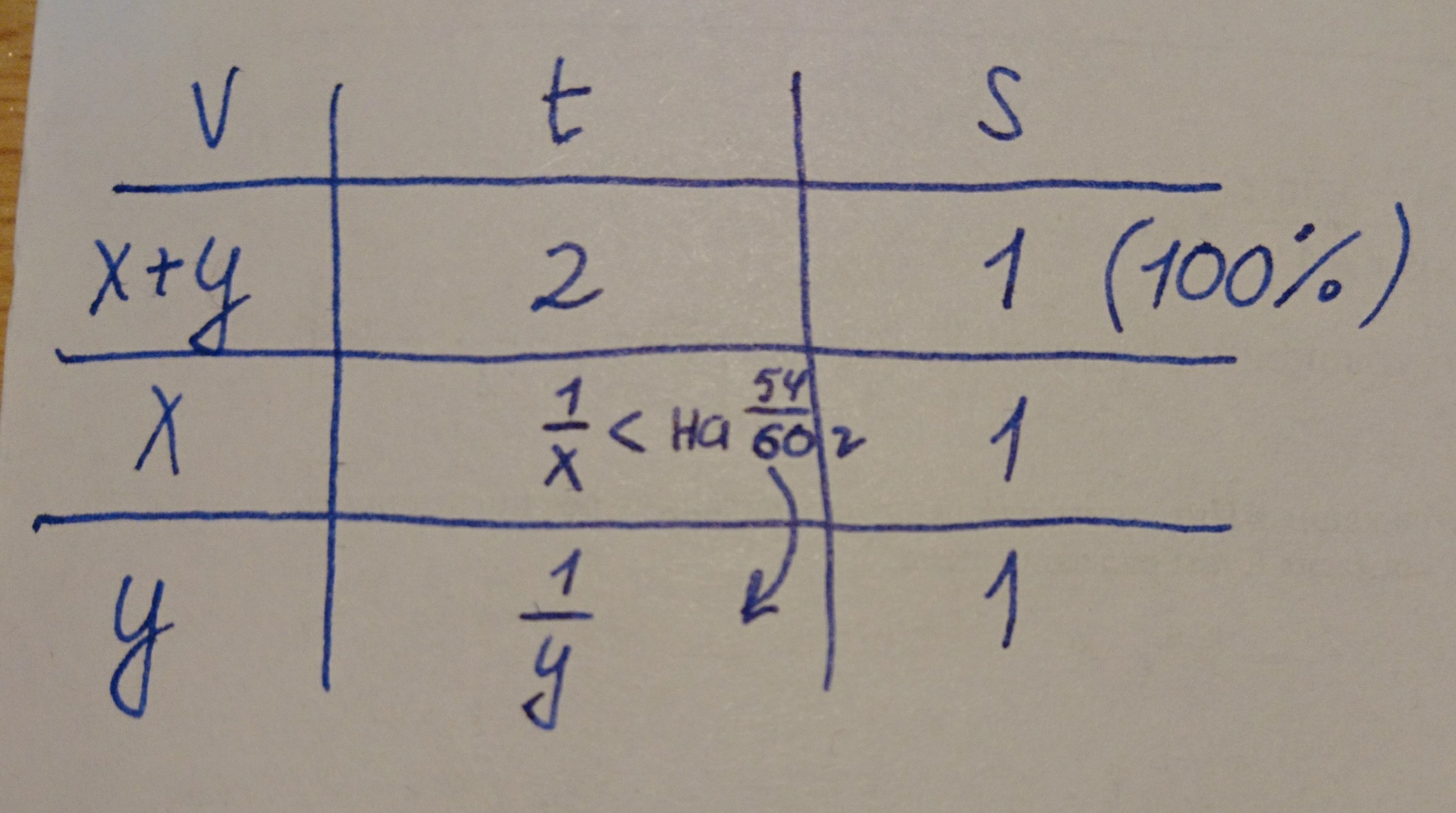
x - скорость первого
y - скорость второго
Весь путь равен 100% = 1
В приложении таблица.


Отдельно решаю 2-е уравнение:
18y²+31y-10 =0
√D = √(961 + 720) = √1681 = 41

y₂ < 0, а скорость не может быть отрицательна ⇒ подходит только y₁
Подставляем y₁ в 1-е уравнение, чтобы найти x:

Ответ: скорость первого пешехода 5/18 км/ч, скорость второго пешехода 2/9 км/ч
y - скорость второго
Весь путь равен 100% = 1
В приложении таблица.
Отдельно решаю 2-е уравнение:
18y²+31y-10 =0
√D = √(961 + 720) = √1681 = 41
y₂ < 0, а скорость не может быть отрицательна ⇒ подходит только y₁
Подставляем y₁ в 1-е уравнение, чтобы найти x:
Ответ: скорость первого пешехода 5/18 км/ч, скорость второго пешехода 2/9 км/ч
Приложения:
Ответ дал:
0
Скорость 1-хкм/ч,скорость 2-укм/ч
{2(x+y)=1⇒x=(1-2y)/2=1/2-y
{1/y-1/x=9/10⇒10(x-y)=9xy
10(1/2-y-y)=9y(1/2-y)
5-20y=9y(1-2y)/2
10-40y=9y-18y²
18y²-49y+10=0
D=2401-720=1681
√D=41
y1=(49-41)/36=2/9 ⇒х1=1/2-2/9=(9-4)/9=5/9
y2=(49+41)/36=2,5⇒х2=0,5-2,5=-2 не удов усл
Ответ скорость 1 пешехода 5/9км/ч,а второго 2/9км/ч
{2(x+y)=1⇒x=(1-2y)/2=1/2-y
{1/y-1/x=9/10⇒10(x-y)=9xy
10(1/2-y-y)=9y(1/2-y)
5-20y=9y(1-2y)/2
10-40y=9y-18y²
18y²-49y+10=0
D=2401-720=1681
√D=41
y1=(49-41)/36=2/9 ⇒х1=1/2-2/9=(9-4)/9=5/9
y2=(49+41)/36=2,5⇒х2=0,5-2,5=-2 не удов усл
Ответ скорость 1 пешехода 5/9км/ч,а второго 2/9км/ч
Приложения:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
10 лет назад
10 лет назад