Решите срочно!!!!))
Дано:
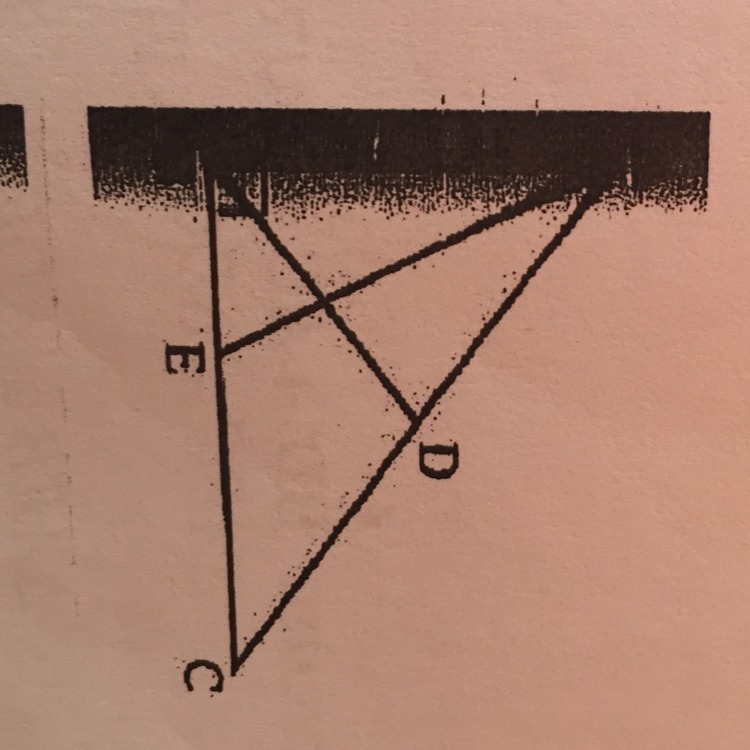
Треугольник ABC-прямоугольный
BD-медиана к стороне AC
AE-половина угла BAC
Доказать:
угол BAE=1/4 угла BDC
Приложения:
Ответы
Ответ дал:
0
Биссектриса АЕ пересекается с медианой ВД - следовательно треугольник равнобедренный. Углы при основании равнобедренного треугольника равны угол С = углу А=45. Медиана является биссектрисой и высотой.
Угол ВДС (90 градусов) является внешним углом треугольника АВД он равен сумме двух внутренних углов треугольника ДВА и ВАД. Они равны по 45 градусов.
Угол ВАЕ равен 1/2 угла ВАД - по условию. Следовательно угол угол ВАЕ равен 1/4 угла ВДС
Угол ВДС (90 градусов) является внешним углом треугольника АВД он равен сумме двух внутренних углов треугольника ДВА и ВАД. Они равны по 45 градусов.
Угол ВАЕ равен 1/2 угла ВАД - по условию. Следовательно угол угол ВАЕ равен 1/4 угла ВДС
Вас заинтересует
2 года назад
7 лет назад
9 лет назад
10 лет назад