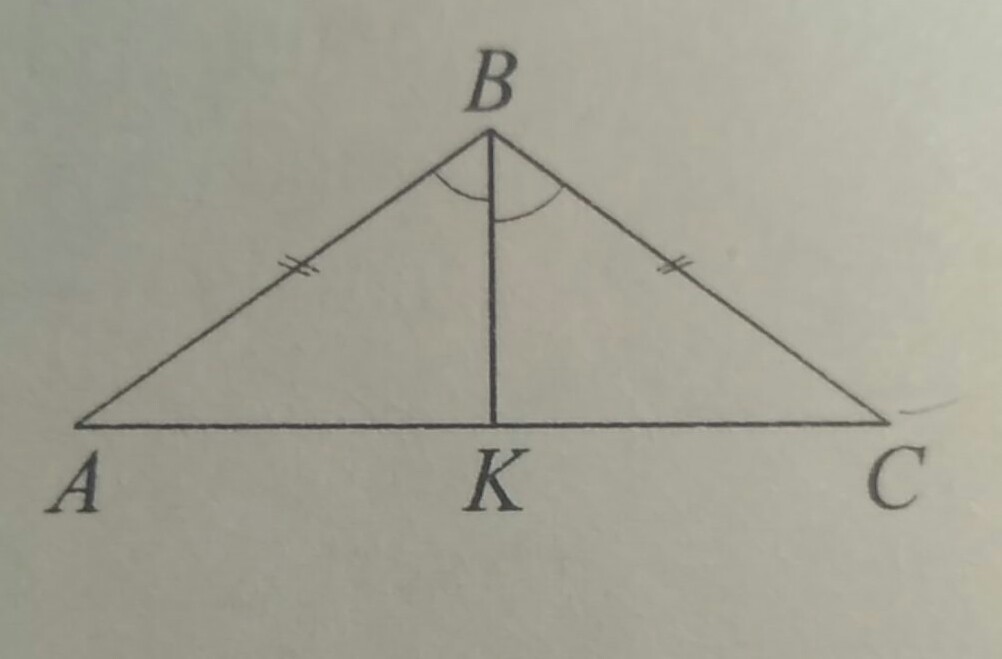
В треугольнике ABC с периметром 70, AB= BC= 18, BK- биссектриса. а) докажите, что треугольник ABK и CBK равны. Б) найдите AK
Приложения:
Ответы
Ответ дал:
0
1) АВ=ВС(за условием)
2) ВК -- общая сторона
Поскольку биссектриса ВК делит угол пополам, то угол АВК = угог КВС.
Следовательно, треугольники АВК и СВК равны за двомя сторонами и прилегающему к ним углом.
АВ=ВС, следовательно, треугольник равнобедренный. У равнобедренного треугольника бессиктриса, высота и медиана совпадают. Значит, АК=КС(медиана делит сторону АС пополам).
1) 70 - (18 + 18) = 34
2)34:2 = 17
АК = 17 см
2) ВК -- общая сторона
Поскольку биссектриса ВК делит угол пополам, то угол АВК = угог КВС.
Следовательно, треугольники АВК и СВК равны за двомя сторонами и прилегающему к ним углом.
АВ=ВС, следовательно, треугольник равнобедренный. У равнобедренного треугольника бессиктриса, высота и медиана совпадают. Значит, АК=КС(медиана делит сторону АС пополам).
1) 70 - (18 + 18) = 34
2)34:2 = 17
АК = 17 см
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад