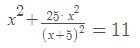Ответы
Ответ дал:
0
В левой части приводим к общему знаменателю:

Введём замену. Пусть , тогда получаем
, тогда получаем

По т. Виета:
Возвращаемся к обратной замене

D<0, то квадратное уравнение ДЕЙСТВИТЕЛЬНЫХ корней не имеет.

Ответ:
Введём замену. Пусть
По т. Виета:
Возвращаемся к обратной замене
D<0, то квадратное уравнение ДЕЙСТВИТЕЛЬНЫХ корней не имеет.
Ответ:
Ответ дал:
0
Поправил ответ
Ответ дал:
0
поправила*
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад