Подскажите пожалуйста как решить это дифференциальное уравнение ч разделяющимися переменными
задание 1.1.10
Приложения:
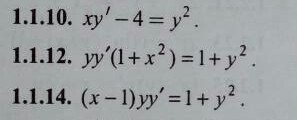
Ответы
Ответ дал:
0
Это дифференциальное уравнение первого порядка разрешённой относительно производной.
Разрешим наше дифференциальное уравнение относительно у'

Получили уравнение с разделяющимися переменными. Разделяем переменные теперь.

Имеем общий интеграл
Разрешим наше дифференциальное уравнение относительно у'
Получили уравнение с разделяющимися переменными. Разделяем переменные теперь.
Имеем общий интеграл
Ответ дал:
0
А есть в виде фото?
Вас заинтересует
2 года назад
2 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад