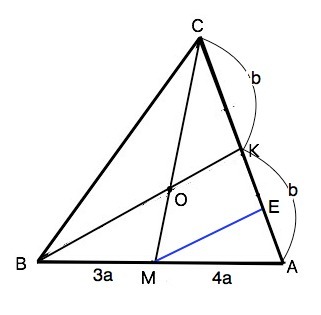
На сторонеAB треугольника ABC указана точка M так что AM:MB=4:3.
В каком отношении медиана BK делит отрезок CM?
Ответы
Ответ дал:
0
Проведем МЕ║ВК. По т.Фалеса в ∆ АВК отношение АК:ЕК=АМ:ВМ=4:3. Отрезок АК содержит 4+3=7 частей. ВК –медиана, поэтому отрезок СК=АК=7 частей
По теореме Фалеса в ∆ МАС отношение СО:ОМ=СК:КЕ. Отрезок КЕ=3 части. ⇒ СО:ОМ=7:3.
Или:
По т.Менелая (АК:КС)•(СО:ОМ)•(ВМ:ВА)=1. (1:1)•(СО:ОМ)•(3:7)=1, откуда СО:ОМ=7/3
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад