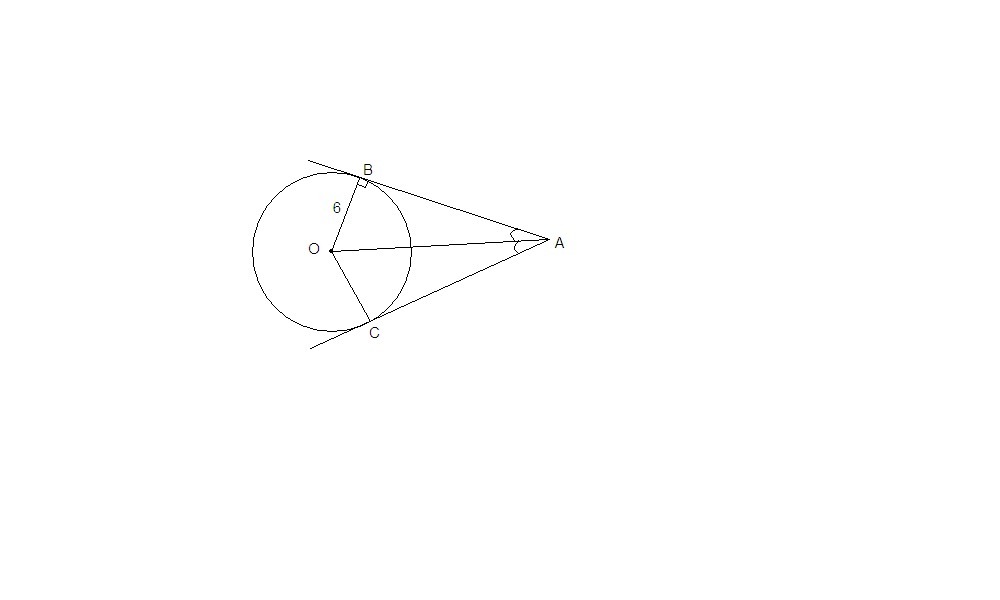
Прямые проходят через точку А и касаются окружности (О,R) в точках B и С. Известно, угол ВАС=60° что и R=6см. Вычислите длину отрезка АО.
Ответы
Ответ дал:
0
Радиус, проведенный в точку касания перпендикулярен касательной.
Значит ОВ⊥АВ, ОС⊥АС.
ΔАОС = ΔАОВ по гипотенузе и катету (АО - общая гипотенуза, ОВ = ОС = R = 6 см)
Тогда ∠ОАВ = ∠ВАС/2 = 60°/2 = 30°.
Катет, лежащий напротив угла в 30° равен половине гипотенузы, значит
АО = 2ОВ = 12 см
Значит ОВ⊥АВ, ОС⊥АС.
ΔАОС = ΔАОВ по гипотенузе и катету (АО - общая гипотенуза, ОВ = ОС = R = 6 см)
Тогда ∠ОАВ = ∠ВАС/2 = 60°/2 = 30°.
Катет, лежащий напротив угла в 30° равен половине гипотенузы, значит
АО = 2ОВ = 12 см
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад
10 лет назад