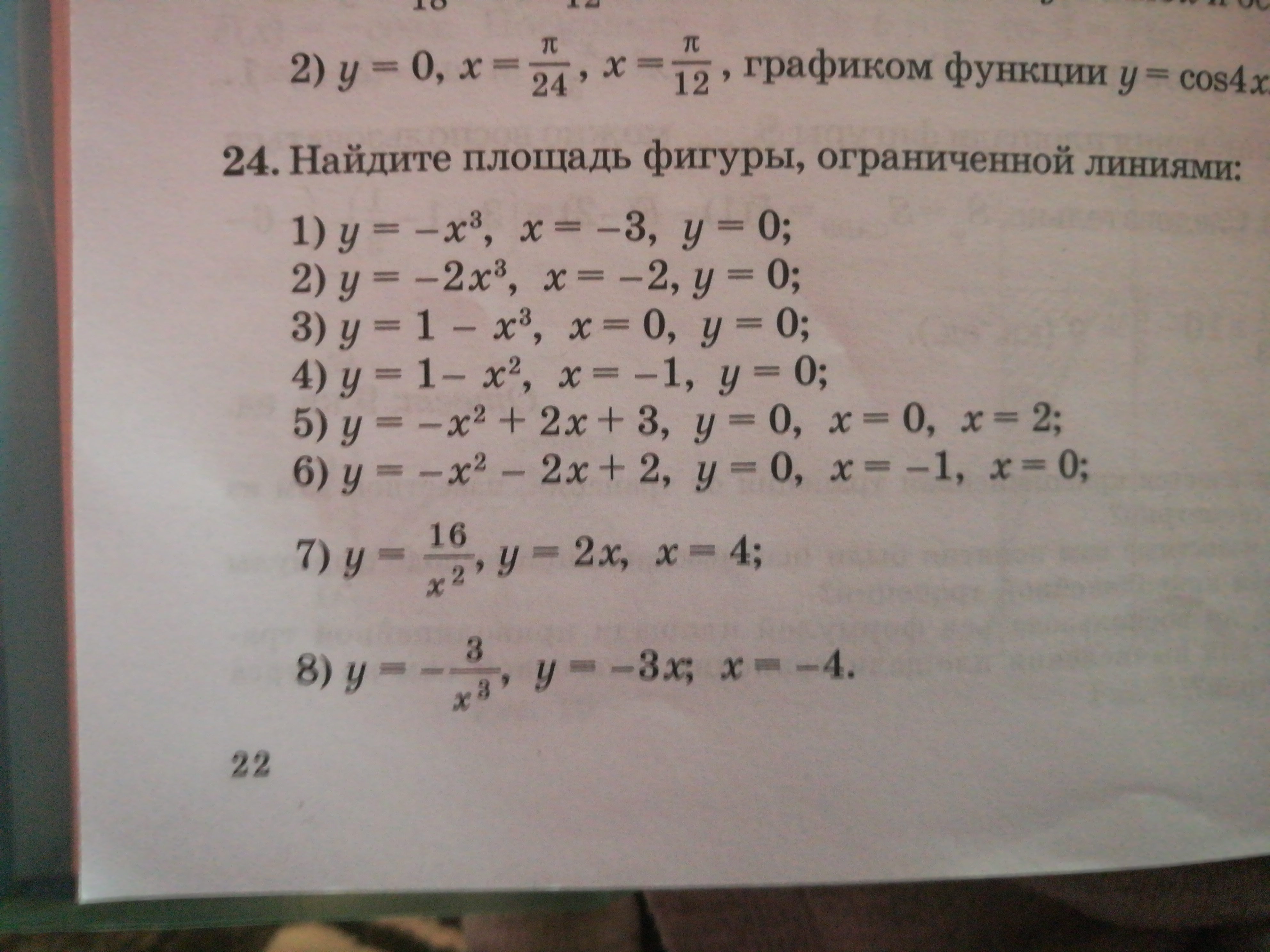Ответы
Ответ дал:
0
х=-3 - прямая, параллельная оси ОУ
у=0 - ось ОХ
2) Аналогичный пример:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад