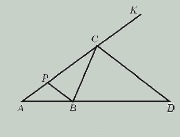
Биссектриса внешнего угла при вершине А треугольника АВС пересекает прямую ВС в точке Д. Доказать что ВД : АВ = ДС : АС
Ответы
Ответ дал:
0
Без проблем
1) BP || CD
2) △APB ∾ △ACD; AC : PC = AD : BD
3) ∠BPC = ∠DCK соответственные при параллельных прямых; ∠PBC = ∠BCD внутренние накрест лежащие; ∠BCD = ∠DCK по условию задачи. ∠CPB = ∠PBC ; △CPB – равнобедренный, т. е. PC = CB.
AD : BD = AC : BC, ДОКАЗАНО!
1) BP || CD
2) △APB ∾ △ACD; AC : PC = AD : BD
3) ∠BPC = ∠DCK соответственные при параллельных прямых; ∠PBC = ∠BCD внутренние накрест лежащие; ∠BCD = ∠DCK по условию задачи. ∠CPB = ∠PBC ; △CPB – равнобедренный, т. е. PC = CB.
AD : BD = AC : BC, ДОКАЗАНО!
Приложения:
Ответ дал:
0
тогда
Ответ дал:
0
по математике
Ответ дал:
0
нет там просто не понятно
Ответ дал:
0
перепутано
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад