Ответы
Ответ дал:
0
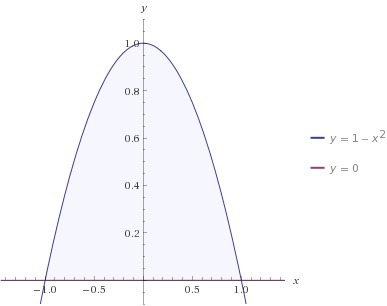
ищем точки пересечения:

Теперь находим площадь с помощью определенного интеграла:

Ответ: ед²
ед²
Теперь находим площадь с помощью определенного интеграла:
Ответ:
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад