Question

найдите наибольшее и наименьшее значение функции f(x) = 2x^(2)-4x+6, если x пренадлежит промежутку [0;3]

Answer 1

Минимальное значение в точке где производная равна 0.
ДАНО
Y(x) = 2x² - 4x +6
РЕШЕНИЕ
Производная функции
Y'(x) =  4x - 4 = 4*(x -1)
Решаем
х - 1 = 0 
х = 1 - минимум функции
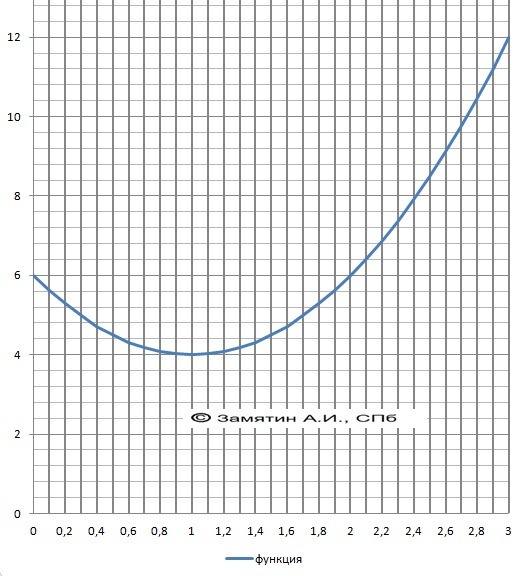
Минимум  Y(1) = 2 -4 + 6 = 4 - ОТВЕТ
Возрастающая парабола - 
Максимум Y(3) = 2*9 - 4*3 + 6 = 18-12+6 = 12 - ОТВЕТ
График в подарок.