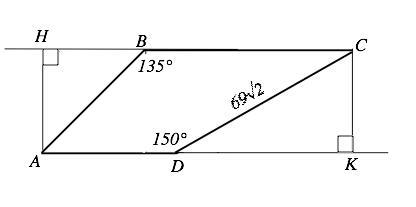
Найдите боковую сторону АВ трапеции ABCD,если углы АВС иADC равны соответственно 135и150 градусов ,а CD=69√2
Ответы
Ответ дал:
0
Ответ: 69 (ед. длины)
Объяснение: Продолжим основания трапеции и проведем к ним перпендикуляры АН к ВС и СК к AD.
Угол СDK как смежный углу АDC равен 30°. По свойству катета, противолежащего углу 30°, СК=CD:2=69√2/2
В ∆ АНВ угол АВН как смежный углу 135° равен 45°. Расстояние между параллельными прямыми равны в любой точке . => Катет АН=СК=69√2/2
Отсюда АВ=АН:sin45°=(69√2/2):√2/2=69 (ед. длины)
Вычислить АВ можно по т.Пифагора из ∆ АВН с тем же результатом.
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
10 лет назад